legislația privind distribuția și caracteristicile de bază ale proceselor aleatoare - studopediya
Să ne amintim că orice caracteristică exhaustivă a variabila aleatoare X - discret, continuu sau mixt este funcția de distribuție a lui F = PX
Acum ia în considerare proces stochastic X (t). Secțiunea transversală a unui proces aleatoriu x (t) pentru fiecare valoare fixă a argumentului t este o variabilă aleatoare care are o lege de distribuție
Această funcție depinde de două argumente: în primul rând, din valorile T. a cărei secțiune transversală este luată; În al doilea rând, valoarea lui x. care trebuie să fie mai mică decât variabila aleatoare X (t). Funcția (6.1), se numește o lege de distribuție unidimensională a procesului aleator X (t).
Pentru procese aleatoare cu stări continue în care fiecare secțiune este o variabilă aleatoare continuă, este posibil să se utilizeze o lege de distribuție diferențial.
Dacă F (t, x) este derivata parțială x
este numit unidimensională sau unidimensional densitatea distribuției proceselor de distribuție a legii diferențiale stocastică X (t).
Este clar că o lege de distribuție unidimensional nu este o descriere exhaustivă a procesului aleator. Funcția (6.1) caracterizează proprietățile oricărui, ci dintr-o singură secțiune. Aceasta nu oferă informații cu privire la distribuirea în comun a două sau mai multe secțiuni.
Pentru a ilustra acest lucru, ia în considerare două proces aleatoriu cu aproximativ aceleași distribuțiilor în fiecare secțiune (figura 6.2). După cum se vede în figură, aceste procese sunt complet diferite structuri probabilistă. În primul rând procesul stocastic (a) are un caracter neted, a avut o relație suficient de strânse între secțiunile. Pentru al doilea (b), această dependență dispare destul de rapid odată cu creșterea distanței dintre secțiuni.
Caracterizarea mai completă a unui proces aleator este o lege de distribuție bidimensională
Funcția (6.3) oferă o idee despre distribuția în comun a două secțiuni selectate aleatoriu - pentru t1 și t2 momente. Dar această caracteristică nu este de două, ci patru argumente, iar utilizarea sa este asociată cu anumite dificultăți, ca urmare a complexității determinarea experimentală a legilor bidimensionale de distribuție, precum și din cauza stângăcie în care se ocupă cu aplicatii.
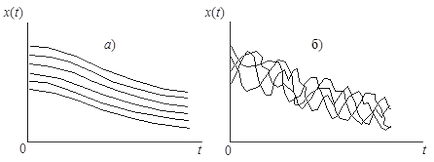
Figura 6.2. Un set de realizări ale două procese aleatoare cu aceleași legi unidimensionale de distribuție, dar având o structură probabilistic diferită.
În general, caracteristica de a fi exhaustivă proces aleator este legea de distribuție n -dimensional. Cu toate acestea, există o clasă mare de procese stocastice (procese Markov) pentru care caracteristica este o lege bidimensională exhaustivă.
În practică, de regulă, în loc de legile de distribuție multidimensionale sunt folosite caracteristicile de bază ale proceselor aleatoare care descriu procesul aleator nu este complet, dar parțial.
Precum și pentru variabila aleatoare am definit speranța matematică, dispersia, momentele inițiale și centrale, precum și pentru un proces aleator vom identifica principalele caracteristici, doar un proces aleatoriu, aceste caracteristici nu sunt numere, și funcții.
așteptarea matematică a unui proces aleator X (t) este numit mx aleatoare (t), că pentru orice valoare a argumentului t este așteptarea matematică a unui proces aleatoriu secțiune transversală corespunzătoare
în care f1 (x t.) - unidimensional densitate de distribuție a procesului aleator X (t).
Astfel, așteptarea procesului aleator reprezintă o anumită funcție „medie“, în jurul căreia variația aleatorie a procesului (figura 6.3).
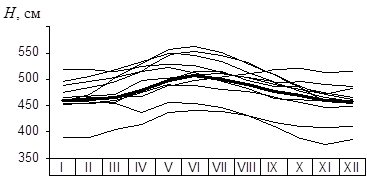
Figura 6.3. nivelurile lunare medii ale lacului Ladoga pentru 1987 - 1988 ani (11) REALISATIONS și așteptări (linie îngroșată).
În cazul în care un proces aleator X (t) să deducă așteptările sale, vom obține centrat proces aleatoriu:
Implementările centrate proces aleator reprezintă abateri de proces aleator X (t) de la așteptările sale. Aceste abateri au valori atât pozitive, cât și negative, iar media este zero:
X (t) a procesului aleator se numește dispersie funcția nonrandom dx (t), că pentru orice valoare a argumentului t este dispersia secțiunii corespunzătoare a unui proces aleator X (t).
Deviația standard a procesului stochastic X (t) este numit sx aleatoare (t), este egală cu rădăcina pătrată a varianței procesului aleatoriu:
sx Funcția dimensiune (t) este egală cu dimensiunea de proces stochastic X (t).
Așteptări și varianța sunt caracteristici importante, dar nu exhaustive ale unui proces aleatoriu, așa cum este determinat de numai o lege de distribuție unidimensional și nu permit să se ia în considerare natura relației dintre secțiunile individuale. Pentru a ține cont de această relație folosind funcția de corelare a unui proces aleator.
Corelare (sau covarianței) funcția unui proces aleator X (t) se numește aleatoare Kx (t, t „), că la fiecare pereche de argument valori t și t“ este egală cu secțiuni transversale corespunzătoare covarianței X (t) și X (t „):
Notă două proprietăți importante ale funcției de corelare:
1. Cu argumente egale (t = t „) este funcția de corelare a varianței unui proces aleatoriu. De fapt,
2. Funcția de corelare Kx (t, t „) este simetrică în raport cu argumentele sale:
Împreună cu funcția de corelare folosind funcția de corelare normalizat.
Normalizează funcția de corelare rx (t, t ') a procesului aleator X (t) este o funcție obținută prin împărțirea funcției de corelare a produsului de deviații standard sx (t), sx (t'):
Proprietățile funcției de corelare normalizate:
1. În cazul argumentelor privind egalitatea t și funcția de corelare normalizat t“este egal cu una din urmatoarele:
2. normalizate funcție de corelare rx (t, t „) este simetrică în raport cu argumentele sale:
3. normalizat funcția de corelare a modulului nu depășește unitatea:
Până acum am vorbit despre procesul de scalare aleatoare, dar există vector de procese aleatoare, în care sunt constituenți pot include două sau proces aleator Bole.
De exemplu, ca un vector de proces aleatoriu poate fi considerată o modificare a cheltuielilor de timp în mai multe calibre.
Pentru a descrie vectorul proceselor aleatoare este necesar să se cunoască așteptările și funcția de corelare pentru fiecare punct al procesului incluse în procesul aleatoriu vectorul ca o componentă. În plus, este necesar să existe o caracteristică care reflectă relația dintre componentele individuale ale vectorului de proces aleatoriu. Ca o astfel de caracteristică este folosită funcția de corelare încrucișată.
Funcția intercorelație Ri, j (t, t ') a celor două procese aleatoare Xi (t) și Xj (t') se numește o funcție aleatorie a două argumente t și t“. la care fiecare pereche de valori ale lui t și t „este covarianța dintre cele două secțiuni ale proceselor Xi aleatorii (t) și Xj (t“):
Enumerăm proprietățile de bază ale funcției de corelare încrucișată:
1. Funcția intercorelație Ri, j (t, t „) nu este, în general simetrice în argumentele sale:
2. Atunci când ambii indici schimbă locurile și argumentele funcției de corelare transversală nu se schimbă:
3. În caz de egalitate indicele i = funcția de corelare reciprocă j este o funcție de corelare a unui proces aleatoriu Xi (t):
procese aleatoare Xi (t) și Xj (t) sunt numite necorelat dacă funcția lor intercorelație Ri, j (t, t „) egal cu zero pentru toate valorile t și t“, cu condiția ca.