L 1 sarcina de a învăța să rezolve inegalitățile și sistemele de inegalități
La soluționarea inegalităților este necesar să ne amintim următoarele reguli.
- în cazul în care ambele părți ale inegalității vom adăuga același număr, noua inegalitate rezultată este echivalentă cu originalul.
- în cazul în care ambele părți ale inegalității înmulțit sau împărțit la orice număr pozitiv, semnul inegalității nu se va schimba.
- în cazul în care ambele părți ale inegalității înmulțit sau împărțit la orice număr negativ, semnul inegalității este inversat.
Capcane №1. Chiar prima capcana care așteaptă rezolvarea inegalităților - este numitorul. O decizie poate fi neglijent să rateze punctul. Pentru a înțelege ce se întâmplă, considerăm această inegalitate.
x + 2 ≥0. Este ușor de rezolvat prin intervale de timp, astfel încât să puteți <=> (X + 2) (5-x) ≥0, deci x = -2 sau x = 5
Aici se încadrează, de asemenea, în capcana! deoarece este imposibil să se împartă cu zero, deci numitorul nu poate fi zero.
Eu propun un alt mod de a rezolva, care va ajuta pentru a evita capcana. Pentru a începe, vom rezolva ecuația
Numărătorul acestei ecuații este zero, numitorul nu este egal cu zero, deoarece la zero delitnelzya!
De fapt, orice inegalitate este de dorit să se decidă trecerea la ecuația. Deși, ca aceasta inegalitate ca [- x <0] нежелательно решать с переходом на уравнение так как при умножении на (-1) мы должны поменять знак, что мы можем упустить из виду при решении уравнения.
Atragem un fascicul de raze pe un punct de notat 2 și 5. Rețineți că punctul umbrită 2 (la fel), iar punctul 5 nu este umbrită (deoarece nu este egal).
Se determină semnele la fiecare interval ușor. Ia punct al intervalului (5 + ∞), exemplul 6 și este substituit în inegalitate (6 + 2) (5-6) = -8 am primit un număr negativ, atunci semnul -. Caracterele rămase sunt alternate. Trebuie să ≥, apoi alegeți un răspuns în cazul în care +.
- În cazul în care inegalitatea semna ≥ sau ≤. paranteza închisă, adică pătrată din [. ]
- În cazul în care inegalitatea semna> sau <. то скобки открытые, то есть круглые (. )
- Dacă ± ∞. bretele este întotdeauna deschisă, adică, (.)
Astfel, răspunsul la scriere [-2, 5).
Să ne rezolve inegalitatea (2-x) 2 (x + 1) (7-x) ≥0. Noi rezolva de intervale.
x = 2 sau x = 1 sau x = 7. grindă Egal și care rezultă punctul de notă fascicul
Definim un semn pe fiecare interval. Luați numărul 8 de pe diferența de drept substitui inegalitatea (8-2) 2 (8 + 1) (7-8) = -324 avansat număr negativ, scrie un minus în acest interval. Supleantul rămase. Aici, atunci vom cădea în capcana.
- În cazul în care trece prin punctul critic, multitudinea de care este egală cu un număr par, partea stângă a standardului nu se schimbă semnul inegalității.
Cum de a evita această capcană?
Rețineți că primul factor are chiar grad care este (x-2) 2
și întotdeauna, în cazul în care există un factor chiar grad în piață sau în al patrulea grad, rădăcina acestei trage buclă și pentru a înregistra minus sau plus comanda intercalare.
Multiplicatorul având un grad chiar este egal cu rădăcina 2, și deci deasupra capsa remiză
și alternanța de semne pentru a scrie un semn minus.
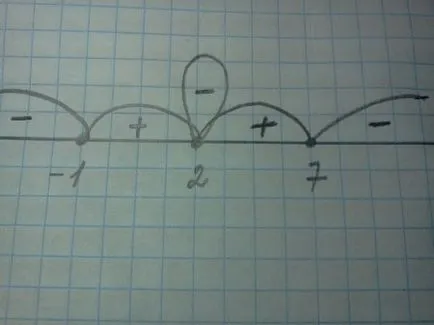
Sa dovedit faptul că, în intervalul [1, 2] și [2, 7] semn nu este schimbat în acest lucru și alte avantaje. Dar, la x = 2, semnul minus, astfel încât acest punct ar trebui să fie excluse. Alegerea lacunele în cazul în care profesioniști.
Să considerăm inegalitatea x 2 + 4x + 4 <0. Его можно решить двумя способами
Găsim discriminantă D = 0, x = -2 parabole în raport cu axa X la un singur punct, dar egal cu zero nu ne interesează, parabola este situat în jumătatea superioară.
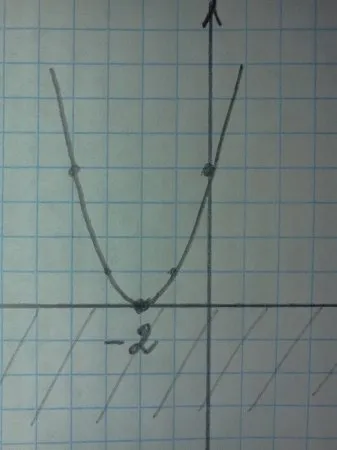
Deci, nu există soluții.
Deviați de la formula x 2 + 4 + 4 = (x + 2) 2. O astfel de expresie nu va fi negativ, ca într-un pătrat.
Există o radacina x = 2. Dar, în același timp, este egal cu zero, nu este inclusă în condițiile cererii.
Prin urmare, punctul nu este umbrită de vopsea. Semnele sunt peste tot profesioniști.
Deci, nu există soluții.
In exemplul anterior, în cazul în care condiția este schimbat la non-strictă inegalitate x 2 + 4x + 4 ≤0. atunci răspunsul va fi numărul unu singur număr.
Să considerăm inegalitatea x 2 + 7 + 5x> 0.
Găsim discriminantă D = -3. Deci, rădăcini. Ce să fac? Capcane.
Parabolei este situat în întregime în jumătatea superioară. Punctele de intersecție cu axa X nu.
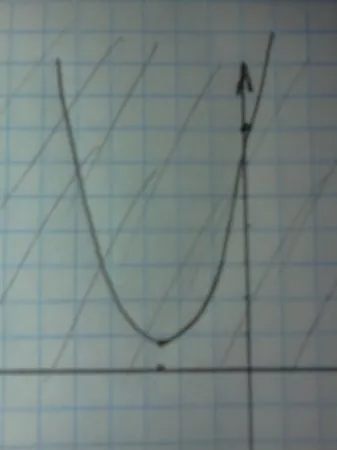
Cerința este mai mare decât zero este îndeplinită în totalitate.
În cazul în care condiția inegalitate schimbare, astfel, x 2 + 5x + 7 <0.Дискриминант отрицательный корней нет. Что делать? Ловушка .
Acum suntem interesați în jumătatea de jos-plan. ci o parabolă situată în întregime în jumătatea superioară. Prin urmare, putem concluziona.
Și acum, să decidă în mod independent următoarele inegalități. Soluțiile vor fi disponibile mai jos.