Interes simplă (p
Analiza fluxurilor de numerar, în cele mai multe cazuri implică calcularea sumei sau a dimensiunii moderne de chirie atrasă.
1.4.2.Formuly suma anuitate obișnuită atrasă
Să presupunem că, la sfârșitul fiecărui an, timp de cinci ani la contul de plătit la ruble R, dobânda se calculează o dată pe an, la rata de i. În acest caz, prima contribuție până la sfârșitul perioadei de creștere a chiriei la o valoare R (1 + i) n-1, un cârlig ca interes sumă R acumulate pe parcursul n-1 an. A doua contribuție pentru a crește la R (1 + i) # 8319; .. ~ 2 etc. Perc-nu sunteți taxat la tranșa finală. Astfel, la sfârșitul chiriei ea rambleu suma va fi egală cu suma unei progresii geometrice:
în care primul termen este egal cu R, numitorul (1 + i), numărul de membri n Această sumă este .:
Se numește compoziția chiriile factorului. Depinde numai de lungimea de închiriere și n rata dobânzii i. Prin urmare, valoarea sa mo-gut să fie prezentate într-un tabel cu două intrări.
În termen de 3 ani de la contul de decontare, la sfârșitul fiecărui an de post-Paet 10 mln. Frecați. , pentru care se calculează în conformitate cu o rată anuală complicată de 10%. Este necesar să se determine valoarea contului curent până la sfârșitul termenului specificat.
chiriile anuale acumulează interes atât de o dată pe an
Să vedem cât de complicat formulă, presupunând că-acum să presupunem că plățile sunt efectuate o dată la sfârșitul anului, iar dobânda acumulată, sunt atât de ori pe an. Acest lucru înseamnă că este utilizat de fiecare dată rate j / m, unde j - rata nominală a dobânzii. Apoi, membrii anuitatea creditate cu-TION până la sfârșitul interes sunt de forma:
Dacă ați citit linia anterioară de la dreapta la stânga, atunci este ușor, dar pentru a vedea că, în fața noastră progresie din nou geometrică, primul membru al cărui este R, numitorul (1 + j / m) m, iar numărul de membri ai n. Suma membrilor acestei progresii valoarea chiriei va atrasă . Acesta este egal cu:
Am găsit suma acumulată, cu condiția ca suma să fie plătită chiria INDICA cartier o dată pe an, în tranșe egale, iar dobanda se percepe o dată la sfârșitul anului. În cazul în care R - valoarea anuală a plăților, mărimea plății departament TION egală cu R / p. Apoi, plățile de secvență nachis-lennymi până la sfârșitul anului de interes, de asemenea, o progresie metrică geo înregistrat în ordine inversă:
în care primul membru al R / p, numitorul (1 + i) 1 / p, numărul total de membri, etc. Apoi rambleu sumă considerată anuitate egală cu suma membrilor acestei progresii geometrice .:
raportul de compoundare rentă p imediat pentru m = 1.
Chirie p-urgent, p = m
Contractele sunt adesea angajamente de interes și primirea doamnei bord coincid în timp. Astfel, numărul de taxe p pe an, iar numărul de taxe la sută m coincid, adică. E. P = m. Apoi, pentru a obține depozite de formula de calcul a sumei pe care se poate utiliza Ana logiey cu atrasă de o chirie anuală și o acumulare de o singură dată de interes, la sfârșitul anului, pentru care:
Diferența este doar în faptul că toți parametrii sunt acum Caracteristici rizuyut-rata și plăților efectuate în cursul perioadei, mai degrabă decât anual. Astfel, obținem:
Acesta este cazul general al chiriei pe termen p cu calculul pro-cenți, astfel ori pe an, și, eventual, P ≠ t.
Primul termen de chirie R / p, plătite după 1 / p ani de la start-La, va fi sfârșitul perioadei, împreună cu dobânda calculată pe ea:
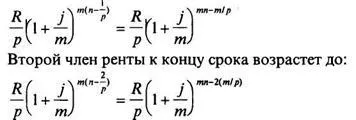
și t. d. a înregistrat acest ultim termen în progresie geometrică inversă este cal-R / p, numitorul (l + j / m) m / p, numărul de membri pt.
Rezultatul este o sumă acumulată:
Rețineți că este ușor să se obțină de la toate cazurile speciale discutate mai sus, stabilind valorile corespunzătoare ale p și r.
1.4.3.Formuly valori moderne.
anuitate ordinară
. Fie un membru al unei rente egală cu R, rata dobânzii i, la sută, sunteți taxat o dată la sfârșitul anului, perioada de chirie etc. Apoi, valoarea-discount MENTULCU prima plată este egală cu:
Reducerea la plata anuitate de sus este egală cu cea de a doua valoare Rv, etc Ca urmare, valorile date formează un pro progresie geometrică -: .. Rv, Rv2, Rv3.Rv“, care este egală cu suma:
-chirie coeficient de reducere.
După cum vom vedea, coeficientul de reducere a chiriei depinde doar de cei doi parametri ai Pas: perioada de chirie n și rata dobânzii i. Prin urmare, valoarea sa poate fi reprezentată sub formă de tabel. Aceste tabele pot fi găsite în cărți sau pe computer pentru a se construi.
Argumente similare permit obținerea unei formule de calcul a valorii actuale a chiriei, în cazul cel mai general pentru valorile pro-arbitrare ale p și m
din care este ușor de a merge la anumite cazuri în diverse district și așa mai departe.
1.4.4.Zavisimost între valoarea curentă și suma acumulată de chirie
Fie A - valoarea curentă a unei postnumerando anuitate, un S - rambleu costurile sale până la sfârșitul perioadei de n, p = 1, m = 1.
Arătăm că dobânda acumulată în valoare de A pentru n ani dă o sumă egală cu S:
Acest lucru implică, de asemenea, că actualizarea dă S A:
un coeficient de reducere (reducere) și con-chirie raporturi de amestecare sunt atașate:
Definirea parametrilor de chirie financiare
Uneori, atunci când în curs de dezvoltare contracte problemă apare definiție TION a predeterminate atrasă suma anuitate S sau moderne Stoi-BRIDGE A rămas parametrii ei de închiriere :. R, n, i, p, t parametri cum ar fi m și p sunt de obicei stabilite prin acordul celor două părți semnatare. Rămân parametrii R, n, i Două dintre acestea sunt stabilite, iar al treilea-rasschity INDICA. Astfel de calcule pot fi repetate de mai multe ori la o dată sau personale valorile parametrilor care, în timp ce nu există nici un acord al părților.
Determinarea cantității mărimea anuală platezhaR
În funcție de caracteristică generală este chiriile constante set S sau A, există două posibilități de calcul:
Definirea chiriei permanente pe termen
Luați în considerare soluția acestei probleme pe un exemplu de anuitate obișnuită cu plăți constante specificate. Rezolvarea inițială ly pentru a forma S și A
. În ceea ce privește termenul n se obțin următoarele două expresii:
Determinarea ratelor dobânzilor
Pentru a găsi rata i, este necesar să se rezolve una dintre ecuațiile neliniare (din nou, presupunând că aceasta este o postnumerando anuitate constantă) următoarele: