identitate logaritmică principal

Identitatea logaritmică principal și logaritm sunt strâns legate.

Identitatea logaritmică principal și logaritm sunt strâns legate. Și, de fapt, identitatea logaritmică principal este o definiție matematică a logaritmului înregistrării. Să examinăm în detaliu ceea ce este logaritmul în cazul în care acesta a avut loc.

Luați în considerare acțiunea algebrică - calculul exponentului x pentru dat valori specifice stepenib și bază a. Această sarcină practic este de a rezolva uravneniyaa x = b, unde a și b - o anumită valoare prestabilită, x - cantitate necunoscută. Rețineți că, în această problemă soluții nu există întotdeauna.

Atunci când, de exemplu, în ecuația a x = bchisloa pozitiv, iar botritsatelno număr. atunci această ecuație nu are rădăcini. Dar dacă a și b sunt pozitive și un ≠ 1, atunci cu siguranță este în mod exclusiv o singură rădăcină. Destul de fapt că graficul funktsiiu exponențială = a x intersectează în mod necesar cu pryamoyu = b și, mai mult decât atât, doar un punct bine-cunoscut. Abscisa punctului de trecere și va fi rădăcina ecuației.

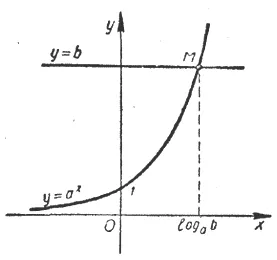
Pentru a indica uravneniyaa x = b rădăcină a utilizat b LOGA (pronunțat: logaritm b în ceea ce privește o bază).

Pe baza definiției, obținem identitatea logaritmică principale:

O consecință a identității logaritmică primare este următoarea regulă.

Din egalitatea a două logaritmi reale obținem o expresie logaritm.

Într-adevăr, atunci când b = LOGA c loga, unde este cazul, b = c.

Luați în considerare de ce logaritmică identităților luate limita a> 0, a ≠ 1, b> 0.

Prima condiție a ≠ 1.

Este bine cunoscut faptul că unitatea este gradul în orice unitate, iar egalitatea x = b LOGA poate exista numai atunci când b = 1. dar log1 1 este orice număr real. Pentru a evita această ambiguitate și a primit un ≠ 1.

Justificați necesitatea unei> 0 condiții.

Când a = 0 prin definiția logaritmului nu poate exista decât în ​​cazul în care b = 0. Și apoi, prin urmare, log0 0 poate fi orice număr real de zero. din moment zero la orice grad nenul este zero. Nu lăsa această ambiguitate dă condiția unui ≠ 0. Dar atunci când un <0 нам бы пришлось отказаться от разбора рациональных и иррациональных значений логарифма. поскольку степень с рациональным и иррациональным показателем определена лишь для положительных оснований. Именно по этой причине и оговорено условие a> 0.

Iar starea finală b> 0 este o consecință a inegalității a> 0. deoarece x = b Loga, iar valoarea bazei cu un rezultat pozitiv întotdeauna pozitiv.