Găsiți intervale de creștere și scădere a funcțiilor derivate în CSE

\ (\ Blacktriangleright \) Dacă derivatul este pozitiv în intervalul \ ((a; b) \). funcția este strict în creștere. \ (F „(x)> 0 \ Longrightarrow f (x) \ upArrow \)

Dacă derivatul este negativ în intervalul \ ((a; b) \). funcția este strict descrescătoare. \ (F „(x)<0 \Longrightarrow f(x) \downarrow\)

Rețineți că Reciproca nu este adevărată. Aceasta este, în cazul în care funcția este strict în creștere pe un interval, atunci nu rezultă că toată această perioadă de derivatul său este pozitiv. De exemplu:

Funcția \ (f (x) = x ^ 3 \), la un interval \ ([- 1, 1] \) este strict în creștere, dar derivatul său nu este pozitiv peste tot: \ (x = 0 \) derivat \ ei (f ' (0) = 0 \) (ca \ (f „(x) = 3x ^ 2 \)).

\ (\ Blacktriangleright \) Dacă funcția nu scade (creșterea și / sau constantă) în intervalul \ ((a; b) \). apoi pe acest interval derivatul său este non-negativ (\ (\ geq 0 \)). Reciproca este adevărată.

\ (\ Blacktriangleright \) Dacă funcția este nonincreasing (scade și / sau constante) în intervalul \ ((a; b) \). apoi pe acest interval derivatul său nu este pozitiv (\ (\ leq 0 \)). Reciproca este adevărată.

\ (\ Blacktriangleright \) la punctele de fractură (în figură acest punct \ (A \) și \ (B \)) derivat nu există.

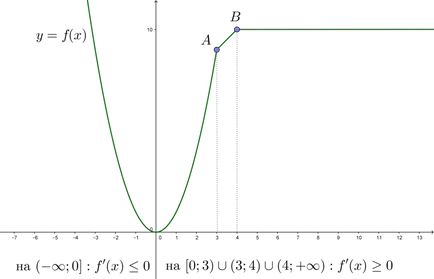
Rețineți că intervalul \ ((4 + \ infty) \) derivat \ (f „(x) = 0 \). deoarece în acest interval este o funcție constantă (\ (f (x) = 10 \)).

Exemplu: obține numărul de puncte la care derivatul este egal cu zero dacă cifra este un caracteristici grafic:

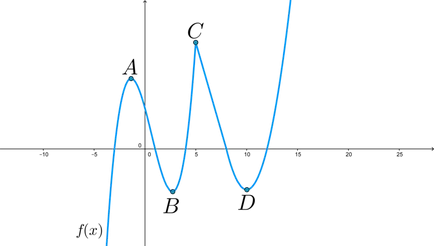
Derivatul este zero la punctele \ (A, B, D \). iar la punctul \ (C \) nu există, deoarece este punctul de fractură.

Lucrări finale sub formă de EGE pentru 11 elevii de clasa conține în mod necesar o referință pentru a calcula limitele și lacunele în scădere ale creșterii funcției derivat, căutarea a punctelor extremum și plotarea. O bună cunoaștere a subiectului face posibil să se răspundă corect la câteva întrebări de testare și nu se confruntă cu dificultăți în formarea profesională continuă.

Bazele de calcul diferențial - una dintre principalele teme ale școlii moderne de matematică. Ea studiază utilizarea derivatelor pentru studiul variabilei dependente - este derivata poate fi analizată creșterea și funcția de scădere fără referire la desen.

pregătire complexă a absolvenților pentru a trece examenul pe portalul educațional „Shkolkovo“ va înțelege profund principiile diferențierii - în detaliu pentru a înțelege teoria pentru a studia exemple de rezolvare a sarcinilor comune și încercați să vă parte la locul de muncă independentă. Vă putem ajuta să umple golurile în cunoaștere - să clarifice noțiunea de concepte lexicale și teme ale variabilelor dependente. Elevii vor fi capabili să repete modul de a găsi intervale de monotonie, ceea ce înseamnă creșterea sau scăderea funcției derivat de la un anumit interval, atunci când punctele finale sunt incluse și nu sunt incluse în intervalele de rezultate.

Alegerea secțiunii „constructor“, elevii vor fi capabili de a practica în studiul de creștere și descreștere a funcției derivate pe versiunile reale de examen sunt actualizate în mod constant pentru a reflecta cele mai recente modificări și inovații.