Găsirea unei funcții obiectiv prestabilit minim
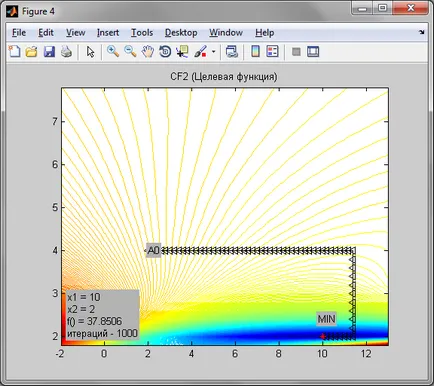
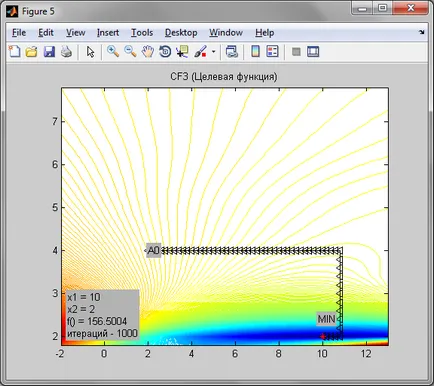
Datorită faptului că metoda de ordinul zero de coborâre, este destul de precisă. Datorită faptului că funcția Rosenbrock are de relief viroaga pentru a atinge punctul minim nu a reușit. punct de oprire în acest caz a fost destul de departe de punctul minim. În cazul punctului de minim funcția elipsă a fost realizată în 21 de iterație, în etapa h = 0,2. In ciuda acestui punct minim funcție obiectiv predeterminat a fost atins exact 91 per repetare, cu pasul h = 0,2 și o precizie de 0,0001.
bibliografie
Fișierul principal al proiectului.
4. ITERATION_AMOUNT = 1000;
5. EPSILON = 0,001; % Precizie
7. POINT_AMOUNT = 50; % Numărul de puncte
punct de pornire 9%
11. x_point_Ellipse (1) = 2;
12. x_point_Ellipse (2) = -2;
14. x_point_Rosenbrock (1) = 4;
15. x_point_Rosenbrock (2) = 3;
17. a1_T_point_CF (1) = 2;
18. a1_T_point_CF (2) = 4;
20.% a și b - valorile pentru raze f II. Elipsă.
24% setările inițiale funcția W (s).
28. ELLIPSE = 'ELLIPSE';
29. ROSENBROCK = 'ROSENBROCK';
32. Partea 1% Euler.
33. y_teor = FirstPart_EulerMethod (a1, T, POINT_AMOUNT);
35% Partea a 2 coordinatewise de optimizare.
36.% funcția [value_of_funct, x] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, a, b, y_exp, number_y_exp, POINT_AMOUNT)
37. [y_Ellipse, x_Ellipse] = SecondPart_OptimizationCoordinate (ELLIPSE, h, EPSILON, ITERATION_AMOUNT, x_point_Ellipse, a, b, -1, -1, POINT_AMOUNT);
38. [y_Rosenbrock, x_Rosenbrock] = SecondPart_OptimizationCoordinate (ROSENBROCK, h, EPSILON, ITERATION_AMOUNT, x_point_Rosenbrock, a, b, -1, -1, POINT_AMOUNT);
40% 3. Partea RNG. CF
41. [CF, a1_T_1, a1_T_2, a1_T_3] = ThirdPart (CF_text, h, EPSILON, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_teor, POINT_AMOUNT);
Funcția metodei Euler.
1. Funcția y_Euler_50point = FirstPart_EulerMethod (a1, T, POINT_AMOUNT)
3. y_Euler la nivel mondial;
5. ITERATION_AMOUNT = 300; % Numărul de puncte pentru primul program.
6. x_t = 5; % Din x referință constantă (t)
11. coeff_z1 = 120 * a1 / T. ^ 2 + 6;
12. coeff_z2 = 6 * a1-120 + 48 * a1 / T;
13. coeff_x_t = 120 * a1 / T. ^ 2;
14.% free_term - termen liber.
15. free_term = coeff_x_t * x_t;
17. pentru i = 1: ITERATION_AMOUNT
18. z1 (i + 1) = z1 (i) + h * z2 (i);
19. z2 (i + 1) = z2 (i) + h * (x_t-z1 (i) -0.4 * T * z2 (i)) / T. ^ 2;
20. y_Euler (i) = coeff_z1 * z1 (i) + coeff_z2 * z2 (i) - free_term;
24.% i = 1: ITERATION_AMOUNT;
26.% titlu (“Y grafic teoretic puncte 300' .);
28.% saveas (GCF, 'ieșire', 'bmp');
29% din rezerva de 300 de puncte numai 50 (POINT_AMOUNT)
31. step_cycle = ITERATION_AMOUNT / POINT_AMOUNT;
32. pentru i = 1: step_cycle: ITERATION_AMOUNT
33. y_Euler_50point (j) = y_Euler (i);
38.% i = 1: POINT_AMOUNT;
titlu 40.% ( 'Y graficul teoretic 50 puncte (fiecare 6).');
Funcția de optimizare coordinatewise
1. Partea 2% coordinatewise de optimizare.
2. Funcția [value_of_funct, x] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, x_start_point, a, b, y_exp, number_y_exp, POINT_AMOUNT)
8. clar (varlist);
14. Deplasare%. pentru a sări peste condițiile de testare out prev. min value_of_funct din ultimele trei sau nu.
15. change_coord = 1;
16% pentru a ieși din bucla dacă numărul. Mai multe iterații ITERATION_AMOUNT.
17. number_iteration = 1;
23. x (1,1) = x_start_point (1); % Prima coordonată, prima valoare.
24. x (2,1) = x_start_point (2); În al doilea rând% coordonate, prima valoare.
25. x (1,2) = x (modificare, i-1) + h; % Prima coordonată, a doua valoare.
26. x (2,2) = x (constant, i-1); % A doua coordonate, a doua valoare.
28. value_of_funct (1) = Ellipse_Rosenbrock_or_CF (function_name, x (1,1), x (2,1), a, b, y_exp, number_y_exp, POINT_AMOUNT);
29. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, x (1,2), x (2,2), a, b, y_exp, number_y_exp, POINT_AMOUNT);
31. dacă new_value_of_function> value_of_funct (1)
33. x (1,2) = x (modificare, i-1) + h;
34. value_of_funct (2) = Ellipse_Rosenbrock_or_CF (function_name, x (schimbare, i), x (constant, i), a, b, y_exp, number_y_exp, POINT_AMOUNT);
37. value_of_funct (2) = new_value_of_function;
40% ciclu până când modulul diferenței funcționează mai epsilon precizie și numărul de iterații este mai mică decât ITERATION_AMOUNT (10000).
41. în timp ce (abs (value_of_funct (i) -value_of_funct (i-1))> EPSILON (number_iteration 43. number_iteration = number_iteration + 1; 45. change_coord = change_coord + 1; 47% se adaugă la prima etapă de coordonate. 48. x (schimbare, i) = x (modificare, i-1) + h; 49% coordonate a doua rescriere. 50. x (constante, i) = x (constant, i-1); 51% găsi valoarea funcției a noilor valori. 52. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, x (1, i), x (2, i), a, b, y_exp, number_y_exp, POINT_AMOUNT); 54% în cazul în care funcția valorile curente mai mult decât o funcție a, atunci h = h * (-1) anterior. în caz contrar value_of_funct (i) = new_value_of_function. 55. dacă new_value_of_function> value_of_funct (i-1) 57% zero afară de ultima valoare 58. x (schimbare, i) = NaN; 59. i = i - 1; % Pentru a reveni la funcția de valoare minimă anterioară % 62. În cazul în care poziția de deplasare ritm făcut nu mai puțin de 3 puncte, apoi prin efectuarea min value_of_funct a ultimilor 3. valori. 63. if (change_coord> = 3) 65% în cazul în care funcția valorilor din etapa anterioară este mai puțin curent și mai puțin în etapa i-2, apoi modificați mișcarea de coordonate. 66. dacă value_of_funct (i-1)> = value_of_funct (i) 68. După% Schimbare coordonate ritm propriu - change_coord zeroize. 69. change_coord = 0; 70. dacă (== constantă 1) 16. value_of_funct = suma ((y_exp (number_y_exp, :) - y_model) ^ 2) / POINT_AMOUNT ;. 20. value_of_funct = -1;