Funcții de putere, rădăcină de cub, o lecție despre algebra în clasa a 9-a, prezentarea
Lecția și prezentarea pe tema: „Funcții de alimentare rădăcină rădăcină cubică Proprietăți cubi ..“
Determinarea funcției de putere - rădăcină cubică
Băieți, vom continua să studieze funcțiile de putere. Astăzi vorbim despre funcția de „rădăcina cub de x.“
Și ce este rădăcina cub?
Numărul y se numește rădăcina cub de x (rădăcina treilea grad), în cazul în care egalitatea $ y ^ 3 = x $.
Ca \ $ Notată sqrt [3] $, unde x - un radicand, 3 - exponent.
$ \ Sqrt [3] = $ 3; $ 3 ^ 3 = 27 $.
$ \ Sqrt [3] = - $ 2; $ (- 2) ^ 3 = -8 $.
După cum putem vedea, rădăcina cub poate fi recuperată de la numere negative. Se pare că rădăcina noastră pentru toate numerele.
Rădăcină cubică a unui număr negativ este un număr negativ. Atunci când ridicarea unui semn păstrat grad ciudat, al treilea grad este impar.
Verificăm că: $ \ sqrt [3] = $ - $ \ sqrt [3] $.
Să $ \ sqrt [3] = a $ și $ \ sqrt [3] = b $. Vom ridica ambele expresii în al treilea grad. $ -x = a ^ 3 $ si $ x = b ^ 3 $. Apoi $ a ^ 3 = -b ^ 3 $ sau $ a = -b $. Rădăcinile notația obținem identitatea dorită.
Proprietăți rădăcini cubice
Să ne dovedesc a doua proprietate. $ (\ Sqrt [3]>) ^ 3 = \ frac ^ 3> = \ frac $.
A primit, numărul de $ \ sqrt [3]> $ tocati este egal cu $ \ frac $ și apoi egal cu $ \ sqrt [3]> $, după cum este necesar.
Băieți, să construiască un grafic al funcției noastre.
1) Domeniul de determinare a setului de numere reale.
2) Funcția este impar, deoarece $ \ sqrt [3] $ = - $ \ sqrt [3] $. În continuare, considerăm funcția noastră ca $ h≥0 $, dupa programul va reflecta cu privire la originea.
3) Funcția crește la $ h≥0 $. Pentru funcția noastră, valoarea mai mare a argumentului corespunde unei valori mai mari a funcției, ceea ce înseamnă o creștere.
4) Funcția nu este mărginită de sus. De fapt, dintr-un număr arbitrar de mare, puteți calcula rădăcina cub, și putem muta până la infinit, sunt găsirea de mai multe argumente de valoare.
5) Cel puțin $ h≥0 valoare de $ este 0. Această proprietate este evident.
Noi construim graficul funcției de la punctele de la h≥0.
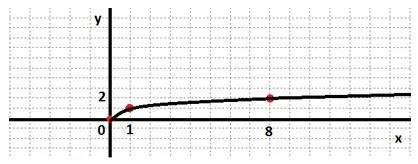
Noi construim graficul nostru a funcției pe domeniul său. Ne amintim că funcția noastră este ciudat.
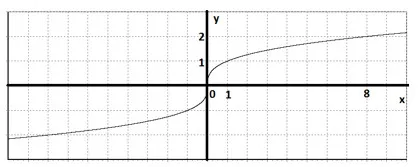
proprietăți funcționale:
1) D (y) = (- ∞ + ∞).
2) o funcție impar.
3) care cresc pe (-∞; + ∞).
4) de închidere.
5) maxime și valorile minime nu sunt prezente.
6) Functia este continua pe linia reală întreg.
7) E (y) = (-∞; + ∞).
8) convexă în jos (-∞, 0) este convex în sus în (0; + ∞).
Exemple de funcții soluții de putere
exemple
1. Rezolva ecuatia $ \ sqrt [3] = x $.
Decizie. Am construit două grafice pe un plan de coordonate $ y = \ sqrt [3] $ și $ y = x $.
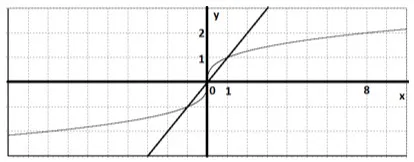
A: (-1, -1), (0, 0), (1, 1).
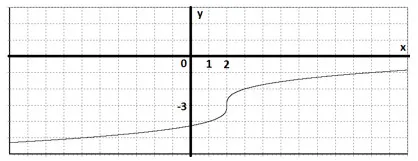
2. Construirea unui grafic al funcției. $ Y = \ sqrt [3] $ -3.
Decizie. Programul nostru se obține din graficul de $ y = \ sqrt [3] $ translație paralelă în două unități la dreapta și trei unități în jos.
3. Se trasează funcția și citiți-l. $ \ Beginy = \ sqrt [3], x≥-1 \\ y = -x-2, x≤-1 \ end $.
Decizie. Noi construim două grafice de funcții pe un plan de coordonate, în conformitate cu condițiile noastre. Când h≥ $ 1 $ am complot rădăcină cub de la $ 1 $ h≤ graficul unei funcții liniare.
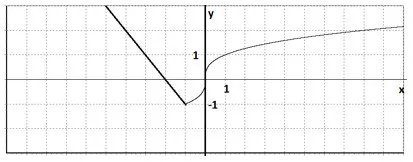
2) Funcția nu este nici măcar, nici ciudat.
3) scade la (-∞, -1), este crescută cu (-1; + ∞).
4) de închidere superioară, mărginită de mai jos.
5) Cea mai mare valoare nu este. Cea mai mică valoare este un minus.
6) Functia este continua pe linia reală întreg.
7) E (y) = (-1; + ∞).
Sarcini pentru decizia independentă
1. Rezolva ecuatia $ \ sqrt [3] = 2 x $.
2. Se trasează funcția $ y = \ sqrt [3] + 1 $.
Graficul 3.Postroit funcției și citi. $ \ Beginy = \ sqrt [3], x≥1 \\ y = (x-1) ^ 2 + 1, x≤1 \ end $.