funcții de analiză exemplu, pentru a parcelei schița

Exemplu funcția de cercetare pentru a parcelei schiță.

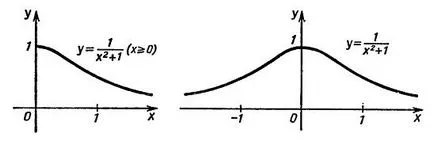
Investigăm funcția f (X) = 1 / (x 2 +1), și în conformitate cu rezultatele trage un calendar schiță.

În primul rând, vom găsi domeniul funcției. Deoarece numitorul nu dispare în nici un x, funcția este definită pe axa reală ansamblu - x poate lua orice valoare. Rețineți că funcția f (x) este chiar, deoarece f (-x) = 1 / ((- x) 2 + 1) = 1 / (x 2 +1) = f (x). Deoarece funcția este chiar, este suficient pentru a investiga și de a construi eskih program doar pentru x pozitive, iar apoi să reflecte ceea ce schita cu axa ordonatei. Acum vom găsi graficul punctelor de intersecție cu axele de coordonate. graficul intersectează punctul (0; f (0)) cu axa ordonatei. Pentru funcția noastră este punctul (0, 1), întrucât f (0) = 1. Pentru a găsi punctul de intersecție cu axa x, este necesar să se rezolve ecuația f (x) = 0. Ecuația 1 / (x 2 +1) = 0 nu are rădăcini reale, atunci graficul f (x) nu intersectează axa abscisă. De aici putem trage concluzia că graficul, fie toate situate pe axa orizontală (funcția de pretutindeni pozitivă) sau dedesubtul întregului (funcția de pretutindeni negativ). Evident, fracțiunea 1 / (x 2 +1) pentru orice X ia valori pozitive, atunci funcția program al întregului nostru situat deasupra abscisă.

În construirea graficul funcției este foarte util pentru a avea informații despre intervalele de creștere și scădere a funcției. Folosind definiția crescătoare și descrescătoare funcții. Acesta poate fi determinat ca f (x) crește în intervalul (-, 0], și scade în intervalul [0;). Astfel, la punctul x = 0 este modificat pentru a crește scăderea funcției. f (0) = 1.

De asemenea, rețineți că, dacă o creștere nedefinită argument numitorul f (x) crește la infinit, astfel valoarea funcției scade la zero (arbitrar aproape de zero). Pe baza funcției de paritate se poate spune că funcția se comportă în același mod și cu scăderea nelimitată în argumentul.

Pe baza informațiilor obținute, putem trage o schiță a graficului, este prezentată în figura de mai jos.