Funcția de transfer Filtru - comunicare si relationare

2.2 Funcția de transfer a filtrului

Ne așteptăm ca funcția de transfer lowpass normalizate prin formula W (P) = N (p) / D (p). Gasim polinoamele N (p) D (p) din tabelele de [1] pentru a comanda filtre Cebîșev II având în vedere că ondulație în passband egală cu 3 dB. obținem:

Facem tranziția inversă a normalizat proiectat la LPF, care transformă funcția de transfer: W1 (P) = N1 (p) / D1 (p), unde

frecvența Scalable: vom face r®wp de substituție / p, în cazul în care Wp = 2p | p = 400P = 1256,64 [rad / s]. Apoi, D1 (p) = D (Wt / p), iar funcția de transfer ia forma:

2.3 Selectarea proiectarea circuitului

În conformitate cu specificațiile tehnice și parametrii calculați ca soluții selectați circuitul HPF-II Sallen-cheie deoarece circuitul are o gamă mică de rating de articole. Procedură întregul filtru n = 2 coincide cu ordinea link-Sallen Key, deci este necesar să se construiască un filtru unitate.

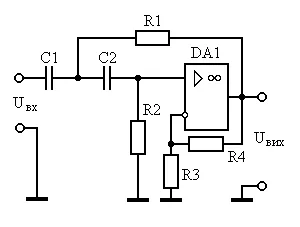
Figura 2.2 - HPF-II, Sallen-Key

3. Modelul topologic și calcularea elementelor de filtrare

3.1 Count Maison FVCH- II.

Compune Earl Maison pentru schemele selectate.

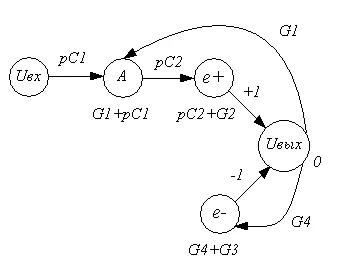
Figura 3.1 - Earl Maison HPF-II

Găsiți funcția de transfer de formula Maison:

Comparabil cu formula pentru canonic HPF-II [2]:

3.2 Calcularea elementelor de circuit

Punerea condensatori capacitate C1 = C2 = 10 / fn = 10 / 0,2 = 50 (nF)

Se determină rezistența rezistorului:

Alegerea rezistenței R3 = 30 ohmi, iar R4 a fost calculată din relația:

Valorile coordonatelor de componente apropiate de E6 standard de:

Setați valorile calculate în circuitul și îndepărtați răspunsul filtrului.

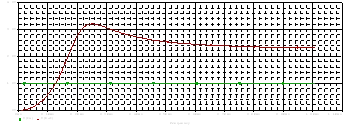
Figura 3.1 - răspunsul de frecvență al filtrului proiectat

4. Metoda de stabilire și ajustare a filtrului

Câștigul filtrului poate fi setat folosind rezistențe R3 și R4 [2]:

Atunci când este utilizat în circuitul amplificator operațional, R3 rezistor poate fi selectată în intervalul de câteva ohmi la 1 Mohm. La o valoare mai mică de R3 devine mai mare curent consumat de circuit și la o mai mare - a face influența lor impedanța de intrare a cip.

Rezistență R4 cu Formula 4.1 se determină pentru câștigul dorit. Având în vedere relația (a se vedea secțiunea 3.2.):

Se poate demonstra că câștigul maxim realizabil în passband este egală cu 3. În acest caz, factorul de calitate maximă a filtrului, dar cel mai mare ondulație prezent în banda de trecere. La încercarea de a crește filtrul Cl și oscilația auto-excitat este transformat în W0 generator de frecvență. Această limită este definită că rezistența R4 este într-un interval de la 0 la 2R3. La circuitul de rezistență zero, devine un filtru Butterworth cu câștig unitate.

w0 Frecvența poate fi configurată cu ajutorul elementelor R1. R2. C1 și C2 [2]:

Cu condiția că R1 = R2 = R și C1 = C2 = C, 4,3 formula simplificată: w0 = 1 / RC. Dacă rezistența și capacitatea nu sunt egale, atunci raportul dintre R1 până la R2 la C1 și C2 este guvernată de factorul de calitate al filtrului. De asemenea, trebuie să se considere că filtrul de mare Q este predispus la auto-excitație.

În cursul acestei lucrări a fost dezvoltat un filtru de înaltă frecvență, cu un ordin al doilea Cebîșev aproximare polinomiala. Acesta constă dintr-o singură legătură Sallen-cheie 2 ordine. Aparatul asigură un factor câștig maxim de 3.2 în passband. Lățime de bandă de frecvență fn = 180 kHz, care este de 10%, diferit de cel dat. Acest lucru se datorează utilizării elementelor de serii standard, E6, denumiri care au o răspândire de 10%. Filtrul permite o simpla reglare a câștig și frecvența de lățime de bandă, și are, de asemenea, un mic elemente cupiuri de variație. Printre deficiențele se numără prezența ondulație în filtre de bandă de trecere inerente cu Cebîșev aproximație.

Sinteza filtrului trece-

Informații despre lucrarea „Sinteza filtru high-pass“