Funcția 14_ekstremumy subiectul mai multor variabile

Funcția EXTREMA de mai multe variabile

ekstemuma atribut necesar.

Definiție: punctul

numit z funcția extremum = f (x, y), în cazul în care valoarea funcției în acest punct, respectiv, mai mare sau mai mică decât valorile asumate de acesta într-un cartier al punctului P0.

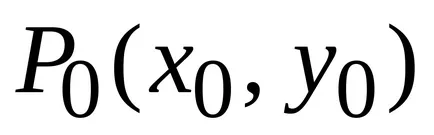
Stabilirea caracteristica dorită sau condiție pentru care funcția ajunge la un punct

extremă.

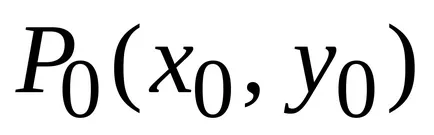
Un criteriu necesar pentru un extremum:

Dacă funcția z = f (x, y) este derivabila x = x0. y = y0, și ajunge la extremum, apoi la acest punct este egal cu zero, a derivatelor sale parțiale:

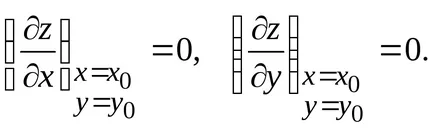
Să presupunem că z = f (x, y) are

extremă. Conform funcției definiția extremum z = f (x, y) la y = y0 constantă ca funcție de x atinge un extremum când x = x0. Premiza pentru aceasta este derivata dispare

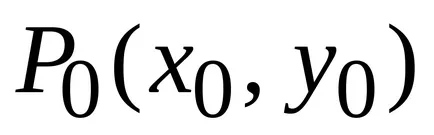
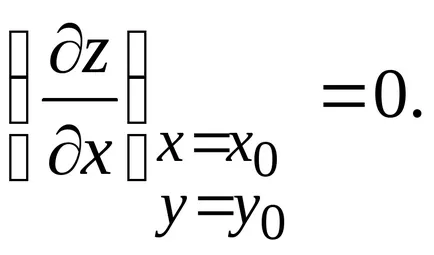
În mod similar, funcția z = f (x, y) la o viteză constantă x = x0. în funcție de y. Se ajunge la un extremum y = y0. așa

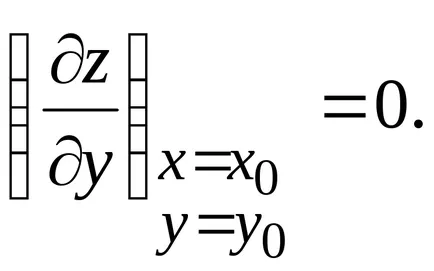
QED.

punct

, coordonatele care dispare ambele derivate parțiale ale funcției z = f (x, y). Se numește punct staționar al funcției z = f (x, y).

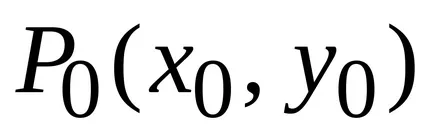
Ecuația planul tangent la suprafața z = f (x, y)

pentru punctul de staționare

primește vidz = z0.

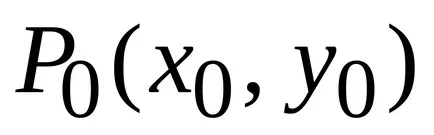
Pentru a găsi punctele de staționare ale funcției z = f (x, y), trebuie să fie ambele egale cu zero, derivatul său parțial

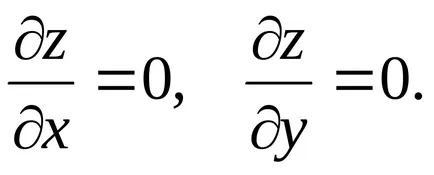
II.Dostatochnye condiții extreme. Să punctul

un punct staționar al funcției z = f (x, y). Calculăm valoarea la acest punct al doilea derivatele parțiale ale funcției z:

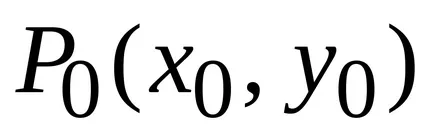
dacă

, atunci funcția f (x, y) are un extremum la punctul P0:

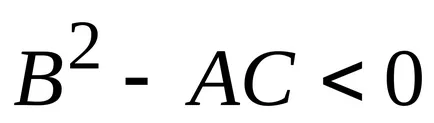
dacă

, nu toP0 un punct de extremum.

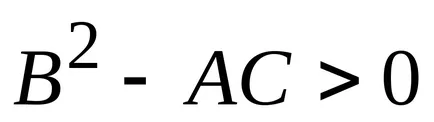
dacă

, atunci nici o concluzie cu privire la natura punctului de staționare nu se poate face, și este nevoie de mai multe cercetări.

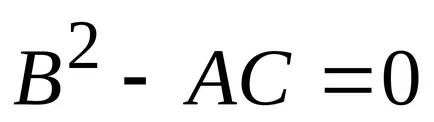
III.Pravila pentru a găsi extreme.

Pentru a găsi punctele extremale și valorile extreme ale funcției z = f (x, y), într-o zonă predeterminată, este necesar:

1) echivalarea derivatelor parțiale la zero

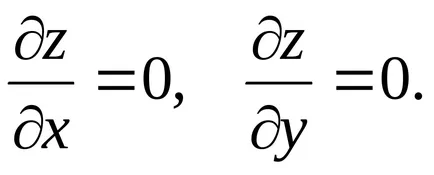
și pentru a găsi rădăcinile reale ale sistemului de două ecuații. Fiecare pereche de rădăcini definește un punct fix al funcției. Dintre toate punctele de staționare pe care trebuie să ia cele care sunt într-o anumită zonă;

2) pentru a calcula valoarea expresiei

,

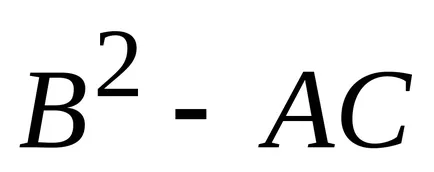
în care în fiecare punct fix.

a) în cazul în care

, atunci avem valoarea extremă: maxim Pria<0 (C<0),

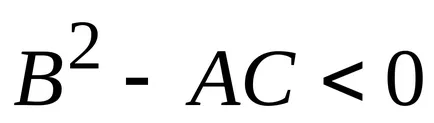
minimă la A> 0 (C> 0).

b) dacă

, atunci nu există nici extremelor;

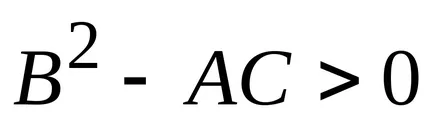
c) dacă

, necesită investigații suplimentare;

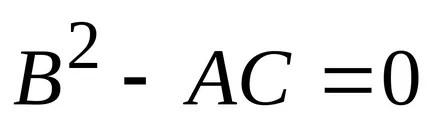
3) se calculează valorile extreme, înlocuind expresia coordonatelor funcționale ale punctelor extremum.

IV.Naibolshee și valorile minime ale funcției.

Să presupunem că vrem să găsim valorile maxime și minime ale funcției z = f (x, y), într-o anumită regiune, luate în considerare împreună cu marginea sa.

Dacă oricare dintre aceste valori se realizează în cadrul funcției de zonă, este în mod evident extremă. Dar se poate întâmpla ca valoarea maximă sau minimă a funcției este luată într-un punct care se află pe granița.

Rezultă din această regulă:

în scopul de a găsi valorile maxime și minime ale funcției z = f (x, y) în zona închisă, este necesar să se găsească toate maximele sau minimele unei funcții care urmează să fie atinse în acest domeniu, precum și cele mai mari sau mai mici valori ale funcției de la limitele câmpului. Cel mai mare dintre toate aceste numere este valoarea dorită cea mai mare și cea mai mică - cel mai mic.

Să o z funcție = f (x, y) și linia L pe 0xy plan. Provocarea este de a găsi pe linia L un punct P (x, y). în care valoarea funcției z = f (x, y) este cea mai mare sau cea mai mică în comparație cu valorile acestei funcții, la o linie L. Aceste puncte sunt numite puncte P constrânse funcția de optimizare z = f (x, y) pe linia L. In contrast, valoarea normală extremum punctul a funcției la extremum condiționată punct este comparată cu valorile nu funcționează la toate punctele de un cartier, ci numai acelea care se află pe linia L.

Evident, punctul extremelor convențional și punctul este constrânsă de optimizare pentru orice linie care trece prin acest punct. Dar punctul extremum condiționate nu poate fi punctul de extremum convențional.

Am găsit un punct de extremum condițional funcția z = f (x, y) pe linia dată de ecuația L.  (x, y) = 0. care se numește ecuația comunicării.

Dacă conexiunea ecuației poate fi exprimată în mod explicit de x y. apoi prin substituirea în ecuația z = f (x, y). Obținem z în funcție de o singură variabilă:

Găsirea valoarea lui x. la care funcția ajunge la un extremum, iar apoi determinarea de constrângerea ecuațiile de valorile corespunzătoare ale lui y. vom obține punctele necesare ale extremelor condiționate.

Sarcina problema extremum condiționată este redusă la găsirea unei extremum a funcției unei variabile, iar dacă ecuația constrângere este dată de ecuațiile parametrice:

Dacă ecuația de constrângere este mai complicată și nu se poate exprima în mod clar o variabilă peste alta, problema de a găsi extremum condiționată devine mai dificilă.

Scriem derivatul total al funcției z = f (x, y) de x

Condiționale puncte extremum ale derivatului totală ar trebui să fie zero. În plus, variabile, și trebuie să satisfacă ecuația de constrângere. Astfel, problema se reduce la rezolvarea unui sistem de două ecuații pentru cele două necunoscute:

.

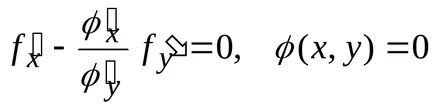
Noi transformăm prima ecuație la forma

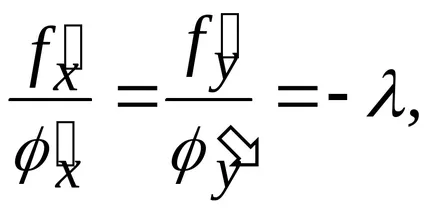
în cazul în care  - un număr real. Apoi am ajuns la cele trei ecuații

pentru x necunoscut. y. .

Ecuațiile (1) mai ușor de reținut folosind următoarele reguli:

în scopul de a găsi puncte care ar putea fi punctele extremum condiționate ale funcției z = f (x, y) în ecuația comunicării  (x, y) = 0. Avem nevoie pentru a forma o funcție auxiliară

unde  = const și stabilite ecuațiile pentru găsirea punctelor extreme ale acestei funcții.

Metoda de mai sus de rezolvare a problemelor se numește metoda multiplicatorilor lui Lagrange.

Sistemul (1) prevede numai condițiile necesare pentru un extremum. Nu orice pereche de x și y (1) este o optimizare constrânsă punct.