expresii de conversie care conțin radicali
§ 42. Conversia expresiilor ce conțin radicali
În clasele 7 și 8 ați finalizat transformarea expresiilor raționale folosind regulile de funcționare pe polinoame și fracții algebrice, formule de multiplicare prescurtate, etc. În clasa a 8-a, ai învățat o nouă operațiune - exploatarea de extragere a rădăcinii pătrate a unui număr non-negativ și, folosind proprietățile de rădăcini pătrate, efectuate expresii converti care implică rădăcini pătrate. În secțiunile precedente am întâlnit cu operația de extragere a rădăcinii gradului nth unui număr real, a studiat proprietățile acestei operațiuni, și anume, (pentru valori non-negative a și b):
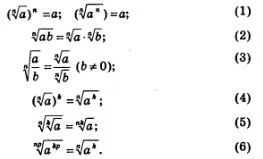
Folosind aceste formule, este posibil să se efectueze expresii de conversie care conțin operații de extracție a rădăcinii (radicali expresii); - expresii numite irațional. Luați în considerare mai multe exemple de expresii de conversie iraționale.
Exemplul 1: Simplificați expresia:
Soluție: a) reprezintă radicand 32a 5 ca 16 și 4 - 2a și utilizați formula (2); obținem:
Expresia rezultată este considerată a fi mai ușor decât setul, deoarece sub radicalul conține mai mult decât o expresie simplă. O astfel de transformare se numește impunerea unui factor ca semn al radicalului.
b) Folosind (4), obținem:
Reprezintă radicand și 10 sub forma unei 9 -a și folosi formula (2); obținem:
După cum vedeți, și aici a fost în măsură să facă semnul Multiplicatorul radicalului.
Amintiți-vă de formula pe care le-ați studiat în cursul algebra în clasa a 8-a. Este generalizat la orice chiar indicele rădăcină
Această formulă ar trebui să se țină seama în acele cazuri în care nu există nicio certitudine că variabilele iau numai valori non-negative. De exemplu, introducerea unui factor pentru semnul rădăcinii în expresie. ar trebui să (în cazul în care semnul x nu este cunoscut) pentru a argumenta după cum urmează:
În plus față de impunerea unui factor ca semn al radicalului, dacă este cazul, utilizarea și transformare, ca să spunem așa, din direcția opusă: introducerea unui factor sub semnul radical. Această transformare, folosim următoarele două exemple.
Exemplul 2. Pentru a compara numărul de
Decizie. Avem:
EXEMPLUL 3 Expresia simplificată
Decizie. Primul factor va face 1 x rădăcină sub semnul treilea grad:
Acum expresia dată poate fi scrisă ca:
Folosind formula (5), putem scrie ultima expresie în forma
Exemplul 4. Efectuați pașii:
Soluție: a) puteți aplica formula de reducere a înmulțirea „diferența de pătrate“:
Folosind formula (6), pentru a împărți fiecăruia dintre indicii rădăcină radicali derivați și radicand este 2; Acest lucru va simplifica în mod semnificativ intrarea:
b) Este posibilă aplicarea formulei de multiplicare prescurtate „cuburi de diferență“:
Exemplul 5. Efectuați etapele:
Soluție: a) Din moment ce se poate multiplica doar rădăcinile același grad, vom începe cu parametrii de ajustare din radicalii disponibile. Pentru această dublă utilizare formula (6):
Acum folosim formula (2):
Rămâne de a face semnul multiplicare pentru radicalul:
b) Prima cale. Transformarea primul factor la rădăcina de gradul 4-a:
A doua metodă. Noi lucrăm mai întâi cu un radicand în al doilea factor. Avem:
Împărțind rădăcina performanței și expresiei radical cu 2, obținem: (formula (6) avem aici au dreptul de a utiliza, ca expresie radicală - un număr pozitiv). Rămâne să se înmulțească rădăcinile pătrate:
Exemplul 6. factorizat:
Decizie. Expresia dat poate fi rescrisă după cum urmează:
Acum vom vedea că este - un pătrat perfect, pătratul diferenței dintre expresiile
În cele din urmă, obținem:
Exemplul 7 Pentru a reduce fracția
Metoda Reshenie.Pervy. Numitorul poate fi transformat după cum urmează:
Deci, există un motiv de a prezenta numărătorul ca o „diferență de pătrate“:
A doua metodă. Noi introducem noi variabile:
Aceasta ne-a dat schimbarea de variabile? Lăsă înlocuiască expresia irațională (cu variabilele x și y) este o expresie rațională (cu variabilele a și b). Și funcționează cu expresii raționale este mult mai ușor decât cu irațional. Avem:
AG Mordkovich Algebra Grad 10
Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.
Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.