Exemple de jocuri matrice în strategii pure și mixte scad matricea ordin de plată -
2.2 Exemple matrice jocuri în strategii pure și mixte Reducerea matrice ordin de plată
Procedura de plată a matricei (rânduri și coloane) pot fi reduse prin eliminarea strategiilor redundante și dominate.
K * se numește o strategie dominată de strategii K **, în cazul în care orice versiune a comportamentului jucător contra relația
unde și - valoarea victorii la alegerea unui jucător, respectiv, strategiile K * și K **.
În cazul în care relația
=
Strategia K * se numește o copie de siguranță în ceea ce privește strategiile K **.
De exemplu, într-o matrice
O matrice de plată dominat și strategii repetarii. A1 este o strategie dominat raport cu strategia A2, strategia B6 este dominată în ceea ce privește politicile B3, B4 și B5 și B5 este o strategie de rezervă în raport cu strategia B4. Aceste strategii sunt jucători selectate, deoarece acestea sunt cunoscute ca fiind pierdute și eliminarea acestor matrice strategii de plată nu afectează determinarea prețului superior și inferior al jocului, a descris această matrice.
Setul de strategii non-dominate, obținute după reducerea dimensiunii matricei de plată, de asemenea, numit Pareto set (după economistul italian Vilfredo Pareto, este angajată în cercetare în acest domeniu)
Exemplu joc soluții matrice în strategii pure
Luați în considerare exemplul de rezolvare a unui joc de matrice în strategii pure, în ceea ce privește economia reală, într-o situație de luptă între cele două companii pentru piața din regiunea de producție.
Două companii fabricarea de produse si va livra pe piata din regiune. Ei sunt singurii furnizori de produse în regiune, prin urmare, determina pe deplin piață a acestor produse în regiune.
Fiecare întreprindere are capacitatea de a produce produse folosind una din cele trei tehnologii diferite. În funcție de calitatea produselor care este produsă de fiecare tehnologie, întreprinderile pot stabili un preț unitar de 10, 6 și, respectiv, 2 unități monetare. Mai mult decât atât, întreprinderile au costuri diferite pe unitatea de producție.
Costurile pe unitatea de producție produsă de fabricile din regiune (CU).
Prețul de vânzare al unei unități de producție, CU
Costul total pe unitatea de producție, CU
Valorile acțiunilor întreprinderii 1, populația dobândită, depinde de raportul prețurilor pentru produsele întreprinderii 1 și întreprinderea 2. Ca rezultat al cercetării de marketing această relație este stabilită și valorile sunt calculate.
Ponderea întreprinderii 1 achiziționate de către populație, în funcție de raporturile de preț produs (Tabelul 1.1.)
Prețul de vânzare al 1 unitate. producție, CU
Ponderea întreprinderii 1 cumparat populație
Conform problemei pe piața regională funcționează doar 2 companii. Prin urmare, ponderea producției celui de al doilea risc, a achiziționat populația, în funcție de raporturile de preț produs poate fi definit ca un minus procentul primei întreprinderi.
Strategii pentru companii din această problemă sunt deciziile lor cu privire la tehnologiile de producție. Aceste decizii determină prețul de cost și prețul de vânzare pe unitate de producție. Problema avem nevoie pentru a determina:
1. Are această problemă a situației de echilibru atunci când alegerea unor tehnologii pentru producerea de produse de ambele companii?
2. Există tehnologii care întreprinderile nu sunt alese în mod deliberat din cauza dezavantajele?
3. Câte produse vor fi vândute într-o situație de echilibru? Care companie va fi într-o poziție avantajoasă?
1. Definiți sensul economic al cote în matricea de plată a problemei. Fiecare companie caută să maximizeze profiturile din producție. Dar, de asemenea, în acest caz, companiile se luptă pentru regiunea din produsele de pe piață. În acest caz, câștigul unei companii înseamnă o pierdere a celuilalt. Această problemă poate fi redusă la un joc de matrice cu sumă nulă. În acest caz, coeficienții câștigurilor va fi valoarea de diferență a profitului companiei 1 și 2 din producția întreprinderii. Dacă această diferență este pozitivă, compania câștigă 1, iar în cazul în care este negativ - predpriyatie2.
2. Se calculează coeficienții de matrice câștiguri de plată. Pentru a face acest lucru, trebuie să determine valoarea profitului societății 1 și 2 din producția întreprinderii. Profitul companiei în această problemă depinde de:
- prețul și costul de producție;
- numărul de produse achiziționate de către populația regiunii;
- a ponderii produselor achiziționate în întreprinderile publice.
Astfel, întreprinderile de profit valoarea diferenței, plata corespunzătoare coeficienților matricei trebuie determinată prin formula (1):
D = p × (S × R1-S × C1) - (1-p) × (S × R2-S × C2) (1)
unde D - valoarea diferenței a venit din producția întreprinderii 1 și 2 întreprinderi;
p - 1 parts societății achiziționate de către populația regiunii;
S - numărul de produse achiziționate de către populația regiunii;
R1 și R2 - întreprinderi prețul de vânzare al unităților 1 și 2;
C1 și C2 - costului unitar total de producție, produse la plante 1 și 2.
Calculăm unul dintre coeficienții matricei de plată.
Să presupunem, de exemplu, compania 1 face o decizie privind fabricarea de produse în conformitate cu tehnologia III, precum și compania 2 - în conformitate cu tehnologia II. Apoi, prețul de vânzare unitar. produse pentru întreprinderea 1 este 2 CU în timp ce costul unitar. produs 1,5 CU Pentru companiile pret 2 de vânzare al unității. producția va fi de 6 CU 4 la un cost de CU (Tabelul 1.1.).
Numărul de produse pe care populația regiunii va dobândi, la un preț mediu de 4 CU egal cu 4 mii. unități. (Tabelul 1.2). Ponderea produselor pe care oamenii achiziționează întreprinderea 1, va fi 0,85, iar întreprinderea 2-0.15 (. Tabelul 1.3). Calculati o plată a32 coeficient matrice cu formula (1): a32 = 0,85 x (4 x 2-4 x 1,5) - 0,15 x (4 x 6-4 x 4) = 0,5 mii unități ..
unde i = 3 - numărul Tehnologia prima întreprindere, și j = 2 - numărul doua tehnologie întreprinderii.
În mod similar vom calcula toți coeficienții matricei de plată. Strategia A1 Matricea de plata - A3 - sunt decizii cu privire la companie de producție de tehnologie 1, strategia B1 - B3 - decizii cu privire la tehnologiile de producție acum 2 cote - 1 diferență între profitul de afaceri și de întreprindere 2. O matrice de plată în joc „Lupta dintre cele două companii pentru piața din regiunea de producție. "
În această matrice, nu a dominat sau strategii care se suprapun. Acest lucru înseamnă că ambele societăți se cunosc tehnologii de producție nefavorabile. Definiți elementele minime ale rândurilor matricei. Pentru întreprinderea 1, fiecare dintre aceste elemente este setat la un câștig minim garantat atunci când aleg o strategie adecvată. Elemente minime în rânduri ale matricei au valori: 0,17, 1,5, 0,4.
Definim elementele maxime ale coloanelor matricei. Pentru întreprindere 2, fiecare dintre aceste elemente este stabilit, de asemenea, payoff minim garantat atunci când aleg o strategie adecvată. Elementele maxime ale coloanelor matricei au valori de 3, 0,62, 0,4.
Valoarea mai mică a jocului în matrice este de 0,4. Prețul de sus al jocului este, de asemenea, egal cu 0,4. Astfel, valoarea inferioară și superioară a jocului în aceeași matrice. Acest lucru înseamnă că există o tehnologie de producție, care este optimă pentru ambele companii în ceea ce privește această problemă. Această tehnologie III, care corespunde strategiei 2. Strategia A3 Compania 1 și Compania B3 A3 și B3 - strategii optime pure în această problemă.
Valoarea diferenței de întreprindere de profit 1 și 2 întreprindere la alegerea strategiei optime pur pozitiv. Acest lucru înseamnă că societatea este de 1 victorie în acest joc. 1 întreprinderi câștig este de 0,4 mii. CU În același timp, pe piața de 5 mii. Unitățile vor fi vândute. ieșire (realizare este cererea de produse, tabelul 1.2). Ambele companii stabilit prețul pe unitate în 2 CU În același timp, compania pentru prima costul unitar total de producție se va ridica la 1,5 MU iar pentru al doilea - 1 MU (Tabelul 1.1). Enterprise 1 va câștiga numai datorită procentului ridicat de produse care achiziționează poporul său.
Strategiile mixte în jocuri matrice
Conceptul de jocuri de matrice cu extensie mixtă
Cercetarea în jocuri matrice începe cu găsirea prețul său net. În cazul în care jocul de matrice are o soluție în strategiile pure, apoi găsind prețul net se termină studiul jocului. În cazul în care jocul nu este soluția în strategiile pure, puteți găsi un preț de jos și partea de sus a jocului, ceea ce indică faptul că jucătorul 1 nu ar trebui să spere un câștig mai mare decât prețul de sus al jocului, și poate fi sigur de a obține câștigul nu este mai mică decât prețurile de joc mai mici . Soluții Îmbunătățirea jocuri de matrice pot fi găsite în utilizarea strategiilor de aplicare să respecte viața privată și posibilitatea de repetare multiplă a jocurilor ca o petrecere. Acest rezultat este obținut prin aplicarea unei strategii pure aleatoriu, cu o anumită probabilitate.
Definiția. strategie mixtă a unui jucător se numește un set complet de strategii pure aplicate pe, în conformitate cu distribuția de probabilitate prescrisă. joc Matrix pentru a fi rezolvate prin utilizarea unei strategii mixte, numit jocul cu extensia mixtă.
Strategia aplicată pe o probabilitate diferită de zero, se numesc strategii active de.
Este dovedit că pentru toate jocurile cu expansiune mixtă mixtă există o strategie optimă în alegerea valorii câștigătoare, care este între prețul superior și inferior al jocului:
VH V £ £ Vc.
În aceste condiții valoarea lui V se numește valoarea jocului.
În plus, se dovedește că, dacă unul dintre jucătorii să adere la strategia mixtă optimă, premiul rămâne același și egal cu prețul de joc V, indiferent de ce strategie să urmeze un alt jucător, dacă nu este dincolo de strategiile sale active. Prin urmare, pentru a obține cea mai mare garanție de a câștiga al doilea jucător, de asemenea, trebuie să rămânem la strategia optimă mixtă.
Soluție de jocuri cu matrice cu metode de extensie mixte de programare liniară
Jocul decizia de matrice cu extensia mixtă - definirea strategiilor mixte optime, care este, pentru a găsi astfel de valori ale probabilității de selecție a strategiilor pure pentru ambii jucători atunci când acestea ating cele mai mari câștiguri.
Pentru joc de matrice taxe cont este prezentat în Fig. 1.1 VH VB ¹. definesc astfel probabilități de selecție valori strategii pentru Player 1 (p1. p2, ..., pm) și 2 player (q1. q2, ..., Qn), în care jucătorii au atins lor payoff maximă garantată.
Dacă unul dintre jucătorii să adere la strategia optimă, atunci, starea problemei, câștigurile sale nu poate fi mai mic decât prețul de V. joc Prin urmare, această problemă poate fi prezentat jucătorilor sub forma următoarelor sisteme de inegalități liniare:
Pentru primul jucător:
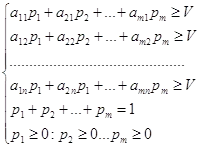
Pentru al doilea jucător:
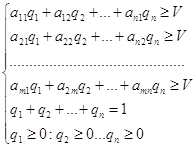
Pentru a determina valoarea V, împărțiți pe ambele părți ale fiecăreia dintre ecuațiile în cantitate V. pi / V este notat cu xi. și qj / V - prin yj.
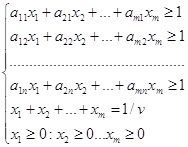
Pentru jucător 1 vom obține următorul sistem de inegalități din care vom găsi valoarea de 1 / v:
1 pentru jucătorul trebuie să găsească valoarea maximă a jocului (V). În consecință, valoarea 1 / V ar trebui să încerce să reducă la minimum.
Funcția obiectiv a problemei va fi următoarea:
Pentru 2 player vom obține următorul sistem de inegalități din care vom găsi valoarea de 1 / v:
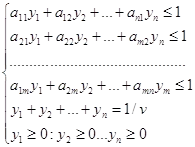
2 pentru jucătorul trebuie să găsească valoarea minimă a jocului (V). În consecință, valoarea 1 / V trebuie să tindă la maximum.
Funcția obiectiv a problemei va fi următoarea:
Toate variabilele din aceste sisteme de inegalități liniare trebuie să fie non-negativ: xi = pi / V, și yi = qj / V. Valorile pi și QJ nu poate fi negativ, astfel cum sunt valorile probabilităților de selecție de strategie jucători. Prin urmare, este necesar ca prețul valorii de joc V a fost negativ. Prețul jocului este calculat pe baza coeficienților de câștiguri matricei de plată. Prin urmare, pentru a asigura starea non-negativitate pentru toate variabilele, este necesar ca toate intrările sunt non-negativ. Acest lucru poate fi realizat prin adăugarea, înainte de rezolvarea problemei pentru fiecare matrice coeficient numărul K, care corespunde modulului cel mai mic coeficient negativ matrice. Apoi, în cursul rezolvării problemei nu este prețul jocului va fi determinată, iar valoarea
Pentru rezolvarea problemelor de programare liniară folosind metoda simplex. [1, 5].
Ca urmare, deciziile sunt determinate de valorile funcțiilor obiective (pentru ambele aceste valori sunt aceiași actori), precum și valorile variabilelor xi și YJ.
Valoarea V * este determinată de formula: V * = 1 / z
probabilități de selecție Valori strategii sunt determinate: pentru jucător 1: Pi = xi × V *: pentru jucător 2: qi = yi × V *.
Pentru a determina prețul de joc din valoarea V V * * trebuie să scădeți numărul K.
Exemplu joc soluții matrice cu extensie mixtă
Să considerăm exemplul rezolvării unui joc matrice cu extensie mixtă. Achitarea Formulări jocuri cu matrice pe baza datelor brute prin înlocuirea unei părți din valoarea întreprinderii 1 achiziționate de către populație, în funcție de raporturile de preț (Tabelul 2.1.).
Tabelul 2.1 - Ponderea întreprinderii 1 dobândite de către populație, în funcție de raporturile de preț produs
Prețul de vânzare al 1 unitate. producție, CU
Ponderea întreprinderii 1 cumparat populație