Evaluări ca variabile aleatoare estimare care rezultă este un caz special al variabilei aleatoare

Scorul rezultat este un caz special al variabilei aleatoare. Motivul este că combinație de valori x din eșantion din întâmplare, deoarece x - variabila aleatoare și, prin urmare, este o variabilă aleatoare și valorile sale set de funcții. Să luăm, de exemplu, x - estimare a așteptărilor:
; = + * 2 (021)
Tocmai am arătat că valorile din observația / th poate fi descompusă în două componente: o parte permanentă a districtului și componenta pur aleatoare Uf
x = p + u (0,22)
Prin urmare,
x = r + și (0,23)
unde d - valori medii de probă și.
Se poate observa că x, cum ar fi x, are ambele componente pur aleatorii fixe și. Componenta sa fixă ​​- p, adică, speranța de x, iar componenta sa aleatoare - și că este valoarea medie a unei componente pur aleatoriu în eșantion.
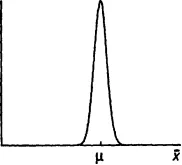
Funcția densității de probabilitate x și x este prezentat în aceleași grafice (fig. 0.7). După cum se arată în figură, valoarea lui x este considerată a fi distribuite în mod normal. Se poate observa că distribuția atât x și x sunt simetrice în raport cu p - media teoretică. Diferența dintre ele este aceea că
distribuția x ca mai sus. Valoarea lui x ar fi, probabil, mai aproape de p
decât valoarea unei singure x observație, deoarece componenta aleatoare este media componentelor pur aleatorii ale u2. SP în eșantion care aparent „stins“ unul de altul la calcularea mediei.

În continuare, amploarea dispersiei teoretice și este doar o fracțiune din teoretic și dispersie. În secțiunea 1.7, vom arăta că, dacă pop. var (i) = a2, apoi pop. var (i) = a2 / L.
Funcția de densitate a funcției densității

probabilitate probabilitate x X

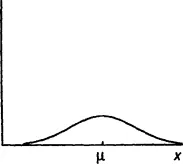
Fig. 0.7. Comparați funcția de densitate de probabilitate a unei singure observare
și proba medie
Valoarea j 2 - estimarea teoretică a varianței x - este, de asemenea, o variabilă aleatoare. Scăzând (0,23) de la (0.22), avem:
xi-x = uj-u. (0,24)
Prin urmare,
* 2 = їІ = - їІ. (0,25)
Astfel, s2 depinde (și numai) este pur componentă aleatorie în observația eșantionului x. Deoarece aceste componente variază de la un eșantion la altul și de la un eșantion la schimbări și valoarea de evaluare s2.