energia cinetică și potențială - studopediya
Energia cinetică a sistemului mecanic - energia mișcării mecanice a sistemului.
F. Forța care acționează asupra corpului în staționare și determinând mișcarea sa, face Rabo, și energia unui corp de vârstă în mișcare este cantitatea de muncă cheltuită. Astfel, forța de funcționare F dA pe corpul Koto-ing pista a avut loc în timpul creșterii vitezei de la 0 la v, este de a crește energia cinetică a corpului dT, r. F.
Folosind a doua lege a lui Newton F = MDV / dt
și înmulțirea ambele părți ale egale TION pe dr mișcare. obținem
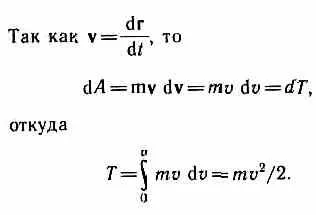
Astfel, masa m un corp în mișcare cu o viteză Xia v, are o energie cinetică
Din formula (12.1) că energia cinetică depinde de masa și viteza corpului, adică. E. Kinetic energie a sistemului este o funcție a stării sale de mișcare zheniya.
In derivarea (12.1) ipoteza sa presupus că mișcarea este considerată un sistem de referință inerțial, deoarece altfel nu ar putea fi utilizate pentru Newton-Kona. În diferite cadre de referință inerțiale care se deplasează în fiecare mente cu privire la alte viteza corpului, și, în consecință, TION, iar energia cinetică va varia. Astfel, energia cinetică-LIC depinde de alegerea sistemului de referință.
Potențial energetic - sistem lic-energie mecanică a corpurilor este determinată de poziția lor relativă și forțele Caracteristici de rom de interacțiune între ele.
Să corpurile de reacție transportate etsya de câmpurile de forță (de exemplu, măsoară domeniul forțelor elastice câmpului forțelor gravitaționale-TION), caracterizat prin aceea că activitatea desfășurată de către o forță de-E atunci când se deplasează corpul unui polo-zheniya la altul, indiferent de plus, o traiectorie se mișcă produ-zoshlo, dar numai pe pozițiile inițiale și finale. Astfel de domenii de legare de potențial și puterea dei le stvuyuschie - conservatoare. În cazul în care activitatea desfășurată de forța depinde de calea corpului de la un punct la altul, o astfel de forță se numește disipativ; exemplul ei este si la frecare.
Corpul este într-un domeniu potențial de forțe are potențialul energetic II. Lucrul forțele conservatoare din elementele-tară (infinitezimale) schimbă configurația sistemului este egală cu creșterea energiei potențiale, luat cu semnul minus, deoarece locul de muncă se face în detrimentul pierderii de energie potențială:
munca dA este exprimat ca un produs scalar al forței F asupra mișcării și dr expresia (12.2) poate fi scrisă ca
Prin urmare, în cazul în care funcția P (r), cu formula (12.3) poate fi găsit forța F în mărime și direcție.
Energia potențială poate fi determinată din (12.3) ca
unde C - .. constantă de integrare, adică, energia potențială este determinat cu o anumită constantă arbitrară este. Acest lucru, cu toate acestea, nu afectează legile fizice, deoarece acestea conțin sau diferență în energiile potențiale ale celor două poziții ale corpului sau P derivat pe coordonate. Prin urmare, potențialul de energie-ing corp în anumite poziții definite evaluat considerate a fi zero (nivel de referință ai Biranne zero), iar energia corpului în alte poziții relative de numărare la nivelul zero. Pentru forțele conservatoare
sau în formă de vector
(I, j, k - vectorii unitare ale coordonatelor-axele). Vector definit expresie-niem (12,5), se numește gradientul ska lyara P.
Pentru el, împreună cu grad notația P, este, de asemenea, desemnarea aplicată ÑAP Ñ ( „Nabla“) se referă la vectorul simbolic, numit operatorul meu-Hamilton nabla sau operatorul:
Forma particulară a funcției P depinde de natura câmpului de forță. De exemplu, într-un potențial energetic al unui corp de masă m, sub-nyatogo o înălțime h deasupra suprafeței Terr-Do, este egal cu
în cazul în care înălțimea h este măsurată de la nivelul zero pentru care P0 = 0. Expresia (12,7) rezultă direct din faptul că energia potențială este egală cu forța de gravitație, atunci când corpul este lăsat să cadă de la o înălțime h la suprafața Pământului.
Deoarece originea este aleasă la întâmplare, energia potențială poate avea o valoare negativă (energie-ki cinetică este întotdeauna pozitiv pe!>. Presupunând că un zero, situată pe suprafața solului a corpului energia potențială, energia potențială a corpului situată în partea inferioară a arborelui (adâncimea h '), P = -mgh'.
Noi găsim energia potențială a corpului deformată elastic (arc). forța elastică este proporțională cu deformare-mațiile:
în care Fxupr - proiecția forței elastice pe axa x; k - coeficientul de elasticitate (un arc - duritate) și minus sign-AUC arată că Fxupr direcționată invers față de deformare x.
Potrivit treia legea lui Newton, forța de deformare-miruyuschaya este egală cu forța elastică modulo și o direcție opusă pe, adică. E.
Fx = -Fxupr = kx lucru elementar dA, realizat de forță Fx cu egalii dx deformare infinit de mic
și munca totală
Este de a crește energia potențială a arcului. Astfel, energia potențială a corpului deformată elastic
Energia potențială a sistemului, sub-BNO energia cinetică este un sistem de stare funcție-TION. Depinde numai la configurația sistemului și sa pus-TION în ceea ce privește organismele externe.
Energia mecanică totală a sistemului, am - energia mișcării mecanice și de interacțiune:
t. e. egală cu suma cinetic și potențial de valorificării potențialului energetic.