Elipsă, geometrie analitică
Definiția 7.1. Setul de toate punctele de pe planul pentru care suma distanțelor la două puncte fixe F1 și F2 au o valoare constantă predeterminată, menționată ca o elipsă.
Determinarea elipsei dă următoarea metodă de construcție geometrică. Reparăm pe planul două puncte F1 și F2. și o constantă non-negativ este notat cu 2a. Lăsați distanța între F1 și F2 este egal cu 2c. Imaginați-vă că șirul inextensibil de lungime 2a ancorat în F1 și F2 puncte. de exemplu, prin intermediul a două ace. Este clar că acest lucru este posibil numai cu ≥. Trăgând creion fir, trage o linie, care va fi o elipsă (fig. 7.1).
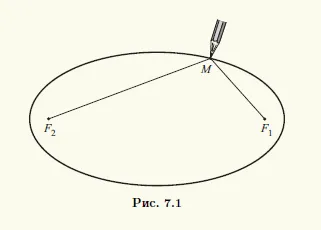
Astfel, setul descris nu este gol, dacă ≥ c. Când a = elipsă reprezintă un segment cu capetele F1 și F2. și atunci când a = 0; , Este o rază de cerc dacă respectiva determinare a elipsă în puncte fixe coincid. Îndepărtând aceste cazuri degenerate, vom continua să predpolat, ca regulă, că> c> 0.
Punctele fixe F1 și F2 ale elipsei în definiția 7.1 (vezi. Fig. 7.1) se numește focarele elipsei. distanța dintre ele, desemnată de 2c, - distanța focală. și segmentele F1 și F2 M M, M conectează un punct arbitrar de pe elipsa cu focarele sale - razele focale.
Vizualizați întregul elipsă definit distanta focala | F1 F2 | = 2c și parametrul a, și poziția acestuia în planul - o pereche de F1 și F2 puncte.
Din definiția elipsei, rezultă că este simetric în raport cu o linie care trece prin F1 și F2 focarele. precum și pe linia dreaptă care împarte segmentul F1 F2 jumătate și perpendicular pe acesta (fig. 7.2, a). Aceste linii sunt numite axele elipsei. Punctul de intersecție O este centrul de simetrie al elipsei, și este numit centrul elipsei. elipsă și punctele de intersecție cu axele de simetrie (punctele A, B, C și D din figura 7.2, a.) - vârfuri ale elipsei.
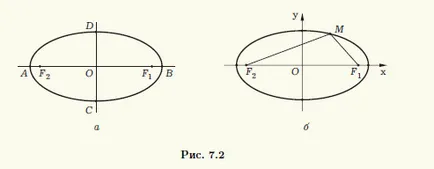
Numărul A se numește axa majoră a elipsei. și b = √ (2 - c 2) - axa minoră. Este ușor de văzut că atunci când c> 0 semimajore axa a este distanța de la centrul elipsei la nodurile care sunt pe aceeași axă ca focarele elipsei (vârfuri A și B din fig. 7.2, a) și axa mică b este distanța de la centrul elipsă pentru sale alte două vârfuri (nodurile C și D din fig. 7.2, a).
Ecuația elipsei. Luați în considerare pe unele elipsă avion cu puncte F1 și F2 focare. axa principală 2a. Lăsați 2c - distanța focală, 2c = | F1 F2 | 2 + y 2) + √ ((x + c) 2 + y 2) = 2a. (7.2)
Această ecuație este incomod, deoarece conține două pătrat radical. De aceea, l-am transforma. Fast forward la ecuația (7.2) din al doilea grup în partea dreaptă, și pătrat:
(X - c) 2 + y 2 = 4a 2 - 4a√ ((x + c) 2 + y 2) + (x + c) 2 + y 2.
După console de expansiune și termeni similari de acționare se obține
√ ((x + c) 2 + y 2) = a + εx
unde ε = c / a. Se repetă operația de cvadratura pentru a curăța și un al doilea radical: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2. sau, având în vedere valoarea parametrului gruparea e introdusă, (2 - c 2) x 2 / un 2 + y 2 = a 2 - c 2. Deoarece 2 - c 2 2 = b> 0, atunci
x 2 / a 2 + y 2 / b 2 = 1, a> b> 0. (7.4)
Ecuația (7.4) satisfac coordonatele tuturor punctelor situate pe elipsei. Cu toate acestea, derivarea acestei ecuații utilizat nonechivalente transformă ecuația originală (7.2) - Doua Cuadratura, Curățirea radicalii pătrat. Construcția ecuației în piața este transformarea echivalentă dacă ambele sale părți sunt valori cu același semn, dar nu am verificat în transformările lor.
Nu putem verifica echivalența transformărilor, dacă luăm în considerare următoarele. Câteva puncte F1 și F2. | F1 F2 | = 2c, în planul definește o familie de elipse la aceste puncte focare. Fiecare punct al planului, cu excepția punctelor segmentului F1 F2. Ea aparține unei familii de elipsă specificat. În acest caz, nu există două elipse nu se suprapun, deoarece suma razelor focale identifică în mod unic un anumit elipsă. Astfel, o familie de elipse așa cum este descris, fără intersecții acoperă planul de ansamblu, cu excepția la punctele de segmentul F1 F2. Luați în considerare setul de puncte ale căror coordonate satisfac ecuația (7.4) cu valoarea parametrului a. Ar putea acest lucru de multe partajate între mai multe elipse? Parte a setului de puncte aparține unei elipse cu semi-axa majoră a. Lăsați acest set este un punct care se află pe elipsa cu axa majoră a. Apoi, coordonatele acestui punct se supun ecuației
și anume Ecuația (7,4) și (7,5) au soluții comune. Dar este ușor să vă asigurați că sistemul
a ≠ un timp nu are soluții. Pentru a elimina acest lucru este suficient, de exemplu, x în prima ecuație:
că după transformare conduce la ecuația
neavând soluții pentru ≠ a, cum. Astfel, (7,4) este ecuația unei elipse cu semi-axei principale a> 0 și axa mică b = √ (2 - c 2)> 0. Se numește ecuația canonică a elipsei.
Forma unei elipse. Metoda de mai sus de construire a unei elipse geometric da o idee bună a formei exterioare a unei elipse. Dar vederea elipsei poate fi studiat cu ajutorul ecuației sale canonice (7,4). De exemplu, este posibil, pornind de la ≥ 0, y exprima prin x: y = b√ (1 - x 2 / a 2), și a examinat graficul funcției se construiesc. Există un alt mod de a construi o elipsă. Un cerc cu o rază centrată la elipsa canonic sistem (7.4) este descris de ecuația x 2 + y 2 = 2. Dacă se coordonează comprima cu un factor de a / b> 1 pe ordonată. atunci obținem o curbă, care este descrisă de ecuația x 2 + (ya / b) 2 = a 2 m. e. elipsă.
Observația 7.1. Dacă același cerc compresa cu un factor a / b 2 - a 2), ε = 2c / 2b = c / b.
Când c = 0, când elipsa devine un cerc, și ε = 0. In alte cazuri, 0 2 - 2) și a = εa = 4, atunci b = √ (5 cu 2 - 4 2) = 3. Atunci ecuația canonică acesta are forma x 2/5 + y 2 2/3 2 = 1. pentru construcția care este o elipsă desena un dreptunghi centrat la cadrul de referință canonic ale cărui laturi sunt paralele cu axele de simetrie ale elipsei și egală cu axele sale corespunzătoare (Fig. 7.4). Acest dreptunghi se intersectează cu

elipsă axe la nodurile A (-5; 0), B (5, 0), C (0; -3), D (0, 3), în care elipsa în sine este înscrisă în acesta. Fig. 7.4 se concentrează, de asemenea, F1,2 (± 4; 0) elipsei.
Proprietățile geometrice ale unei elipse. Am rescrie prima ecuație în (7.6) sub formă de | F1 M | = (A / ε - x) ε. Rețineți că valoarea unei / ε - x a> c este pozitiv, deoarece focalizarea F1 nu aparține unei elipse. Această valoare reprezintă distanța până la o linie verticală d: x = a / gruparea e din punctul M (x, y), situată în partea stângă a acestei linii. Ecuația elipsei poate fi scrisă ca
Aceasta înseamnă că această elipsă constă în acele puncte M (x; y) (. Figura 7.5) ale planului, pentru care raportul dintre M raza focală F1 la distanța până la linia d este o constantă egală cu gruparea e.
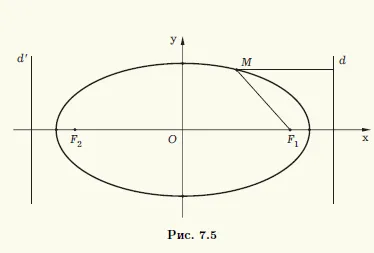
In d direct este „dublu“ - o linie verticală d“, d în raport cu centrul de simetrie al elipsei, care este dată de ecuațiile x = s / £. Relativ d „elipsei este descrisă ca și relativa d. Ambele linii d și d „sunt numite directrices ale elipsei. Directricea elipsei perpendicular pe axa de simetrie a elipsei pe care focii și distanțat de centrul elipsei și o distanță / ε = a2 / s (a se vedea. Fig. 7.5).
Distanța P de directoarei la cel mai apropiat de acesta este numit centrul focal al parametrilor elipsă. Acest parametru este
p = a / ε - c = (2 - c 2) / c = b 2 / c
Elipsa are o altă proprietate geometrică importantă: razele focale F1 F2 M și M reprezintă o tangentă la elipsă la punctul M unghiuri egale (Figura 7.6.).
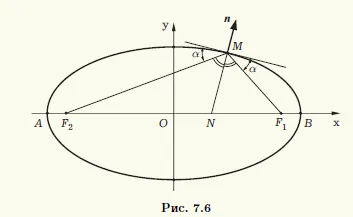
Această proprietate are o semnificație fizică clară. Dacă focalizarea F1 poziționată sursa de lumină, fasciculul în curs de dezvoltare din această concentrare după o reflecție de-a doua elipsa va raza focală deoarece după reflexie va fi la același unghi față de curba ca înainte de reflecție. Astfel, toate razele provin din focalizare F1. se va concentra la a doua focalizare F2. și vice-versa. Pe baza acestei interpretări a proprietății de mai sus se numește o proprietate optică a elipsei.