Determinarea ratei dobânzii efective
Rata dobânzii efective - este o rată a dobânzii complexă calculată pe baza ipotezei că toate plățile necesare pentru a obține acest împrumut, du-te la răscumpărarea lui.
Aceasta este, în cazul în care rezultatul mărimea creditului debitorului trebuie să facă S0 platezhiR0, R1, R2. .rn in puncte vremenit0 = 0, t1, t2. respectiv tn (care include atât plățile pe împrumut în sine și partea Comisiei, plățile de asigurare, etc.), dobânda efectivă este relația stavkai
Rata dobânzii efective este utilizat în principal pentru compararea diferitelor oferte bancare, precum și calculul său de data exactă a plăților de comision sunt, de obicei necunoscute. Prin urmare, în cazul în care plățile sunt efectuate printr-o intervale regulate formale, durata T (lunar, trimestrial, etc.), cu formula (18.1) ia forma următoare:
În cazul în care împrumutatul toate plățile, cu excepția, poate, chiar primul, același (R1 = R2 = = Rn = R.), Apoi, în conformitate cu formula (17.4) pentru determinarea raportului ratei dobânzii efective va fi:
Din păcate, găsirea valoarea exactă a ratei dobânzii efective, chiar și în acest caz, relativ simplu este imposibil, deci trebuie să-l selectați (cel mai bun mod - folosind o metodă numerică specială). Cum anume - acest lucru va fi discutat în paragrafele următoare.
De exemplu, împrumutul cu următoarele condiții:
credite pe termen - 3 ani;
Rata dobânzii (vom nota j ei) - 18% pe an;
schema de rambursare - lunar egal (fix) la cheltuieli;
pentru taxa de acord de împrumut - 1% din suma;
taxă lunară pentru menținerea contului de împrumut - 0,1% din valoarea creditului
Rata efectivă a dobânzii ar fi 22,8%. Pentru a testa găsi valorile tuturor variabilelor prezente în formula (18.3):
Substituind aceste valori în (18,3), după o reducere a S0 ușor pentru a verifica validitatea egalității (cu excepția cazului, desigur, a ignorat eroarea de rotunjire):
Verificați corectitudinea calculului ratei dobânzii efective, puteți utiliza calculatorul nostru de împrumut.
Exemplu de împrumut de 24 de mii de euro, a emis doi ani, la 12% pe an, rambursabil în rate lunare, în conformitate cu schema diferențiată. Taxele de aranjament de 1% din suma. În plus, în fiecare lună debitorul va plăti taxa pentru menținerea contului de împrumut de 0,1% din valoarea creditului. Trebuie să găsim o rată a dobânzii efective a creditului.
În primul rând, vom construi graficul de rambursare a creditului (cu excepția structurii de plată). În § 11, știm că plățile din contul de rambursare a împrumutului formează o progresie aritmetică cu termenul inițial
A1 = 124 + 0,12⋅112⋅24 000 = 1240 euro
-0,12⋅112⋅24 000⋅124 = -10 euro.
În plus, atunci când se aplică pentru un împrumutat de împrumut a trebuit să plătească 0.01 · 24 = 240 000 euro, și în fiecare lună cu el taxă suplimentară de 0,001 · 24 = 24 000 de euro. Prin urmare, programul de plăți asupra creditului este după cum urmează:
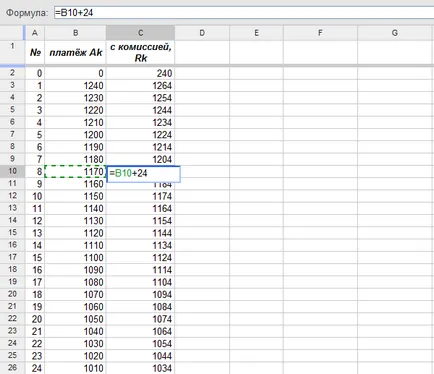
Valorile coloanei „cu comisia, Rk». cu excepția primului (index 0) coincid cu coeficienții funcției f la stepenyahx (x), pe care le vom folosi în calcule. Pentru primul coeficient (zero stepenix) necesar din platezhaR0 = 240 mărimea creditului inițial de scădere (formula la stânga sus):
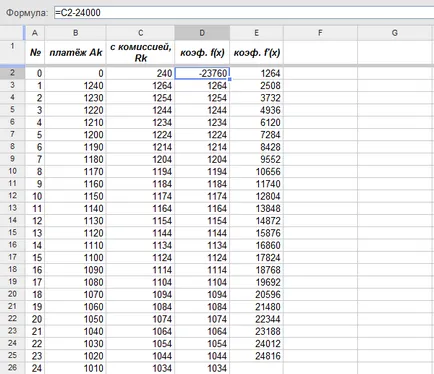
Amintește, dacă cineva a uitat că un număr de coeficienți k al coeficientului derivat este egal cu 1 la funcția nomeromk f (x), înmulțit nak +1.
Acum, în cele din urmă, puteți folosi metoda lui Newton pentru a găsi un factor de reducere lunar (cu formula în colțul din stânga sus):
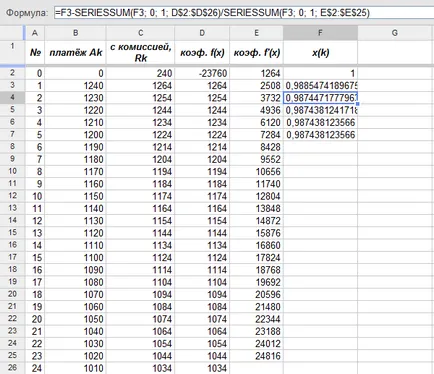
Concomitent cu calcularea factorului de actualizare lunară se definesc rata efectivă a dobânzii i:
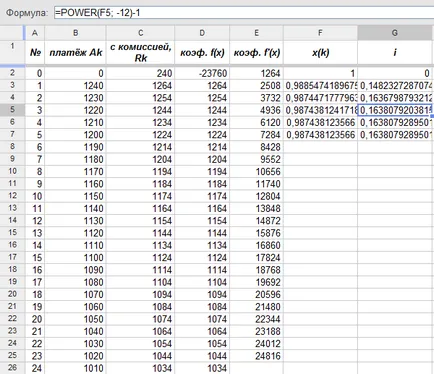
Ca și în exemplul din paragraful anterior, metoda lui Newton ne-a adus răspunsul final la doar cinci calcule: rata efectivă a dobânzii la împrumut în cauză este egală cu aproximativ 16,38%, 4,38% mai mare decât rata nominală.