Determinarea momentului de inerție al unui pendul fizic
Determinarea momentului de inerție al unui pendul fizic
Numele și inițialele Grupa _____________ ______ ______ Data
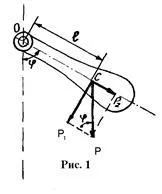
pendul fizic numit fortificat la o axă orizontală fixă nu trece prin centrul de greutate, și capabil să oscileze în jurul acestei axe (Fig. 1)
Gravitatea pendulului fizic P poate fi considerat atașat la centrul de greutate al pendulului S. deviate la un unghi mic # 966; din poziția de echilibru, va
Semnul minus înseamnă că forța de acționare este îndreptată în jos unghi # 966; .
Momentul acestei forțe în raport cu axa de rotație este egală cu
Sub influența acestui punct, corpul dobândește accelerația unghiulară. egală. în cazul în care I - moment de inerție în jurul axei de rotație.
Substituind această expresie în locul valorii M (1) i. Obținem.
Comparând această expresie cu ecuația de oscilații armonice. puteți scrie. dar. înseamnă. în cazul în care:
Ordinea de performanță
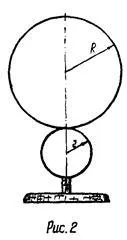
1. Ca un pendul fizic, momentul de inerție trebuie determinată, cele două sunt lipite împreună cu un disc metalic (Fig. 2). Ambele discuri pot oscila în jurul unei axe care trece prin centrul unui disc mare. Folosind rigla milimetri pentru a măsura diametrul și grosimea mari și mici discuri, și cunoscând densitatea discurilor de material (7,8 · 10³ kg / m³) pentru a calcula greutatea fiecărui disc de formula:
unde g = 9,81 m / s².
2. Centrul de greutate al celor două discuri este determinată de următoarele considerente: un disc centre goale sunt situate pe aceeași linie orizontală. Pentru centrul de greutate al fiecărui disc, situate în centrele discurilor sunt aplicate P1 și P2 puterea gravitației. Razele R disc și r.
Centrul de greutate al sistemului format din două discuri, este situat la punctul C. care se află la o distanță # 8467; punctul P2 aplicarea forței și la o distanță de R = r - # 8467; din punctul de aplicare a forței P1. Din legea egalității de momente de arme cu privire la centrul sistemului P2 gravitate # 8729; # 8467; P1 = (R + r - # 8467;) este determinată de distanța # 8467; de axa de rotație a centrului de greutate
3. Respingerea pendulului la un unghi mic, eliberați-l și lăsați-l să se balanseze liber. Se măsoară timpul t 20 oscilații complete și pentru a determina T. perioada de oscilație
unde n - numărul de oscilații complete de.
4. Cunoscând perioada pendulului și greutatea lui P = P1 + P2. determinarea momentului de inerție al pendulului conform formulei:
5. Toate datele sunt înregistrate în tabel
1. Ceea ce se numește fluctuații?
2. Care sunt numite oscilații armonice?
3. Ce se spune amplitudine, faza, faza inițială, o perioadă a frecvenței de oscilație ciclică?
4.Risunok oscilații armonice. Cifra arată amplitudinea, perioada, o fază inițială.
5. Care sunt numite pendulul fizică și matematică?
6Zapishite ecuația oscilații pendul fizic.
fluctuații 7.Ce se numesc libere?
8. Cum se numesc forță cvasi-elastică? Prin ce forțează vibrațiile corpului apar în lucrare?
9.Pri orice pendul fizic fluctuant poate fi considerat armonic?
10. Ceea ce se numește lungimea redusă a pendulului fizic?
11. Cum se schimbă frecvența de oscilații naturale ale unui simplu oscilant pendul cu creșterea greutății corporale de două ori? cu o creștere a lungimii de două ori? Același lucru pentru pendulul fizic.
12. Cum se schimbă energia cinetică, potențială și totală a unui pendul simplu în timp?