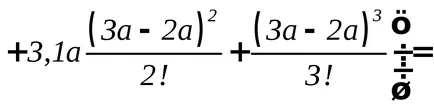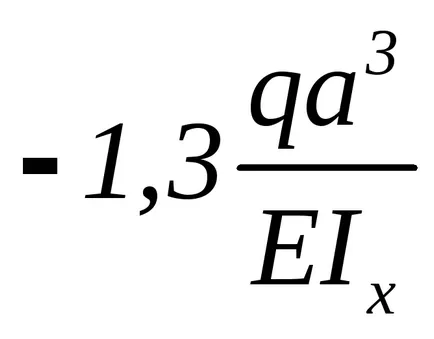Determinarea deformării în încovoiere fasciculului

Deformarea grinzilor de îndoire. Ecuația diferențială a unei axe grindă curbată. Metoda parametrilor inițiali. Ecuația universală a liniei elastice.

6. Deformarea grinzilor sub plane îndoire

6.1. Concepte de bază și definiții

P

Să luăm în considerare deformarea fasciculului la îndoire avionul. axa fasciculului este îndoit de sarcină în planul forțelor (ploskostx 0Y), în care secțiunile transversale sunt rotite și deplasate de către o anumită sumă. Axa fasciculului Twisted se numește o axă curbă elastică incovoiere sau linie.

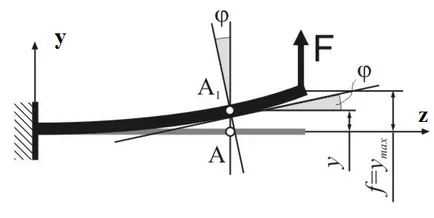
Deformarea grinzilor de flexiune va fi descrisă de doi parametri:

deformarea (y) - deplasarea centrului de greutate al secțiunii transversale grindă într-o direcție perpendiculară

Fig. 6.1 axa sa.

A nu se confunda cu deformarea y coordonate y puncte ale secțiunii fasciculului!

Deformarea maximă a fasciculului se numește încovoierii (f = ymax);

2) rotația unghiului secțiunii () - Unghiul la care secțiunea transversală este rotită în raport cu poziția sa inițială (sau unghiul dintre tangenta la linia elastică și axa fasciculului original).

În general, valoarea deflexie fasciculului la un punct dat este o funcție de coordonatele și z pot fi scrise ca următoarea ecuație:

Apoi, unghiul dintre tangenta la axa curbată a grinzii și axa x se determină din următoarea expresie:

.

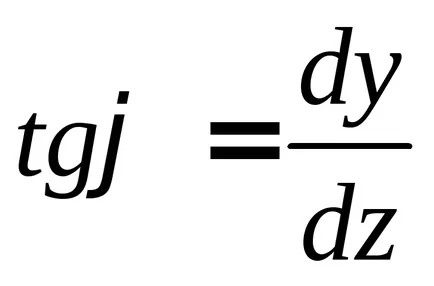
Având în vedere dimensiunea redusă a unghiurilor și deplasărilor, putem presupune că

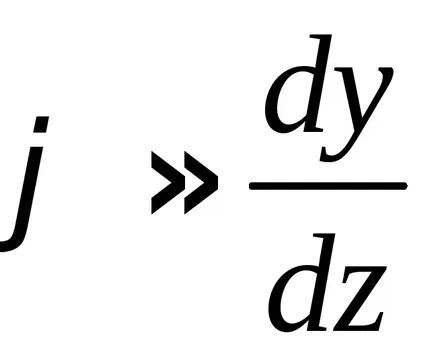
unghiul de rotație al secțiunii este prima derivată din deformarea fasciculului de-a lungul secțiunii abscisă.

6.2. Ecuația diferențială a unei axa fasciculului curbe

În funcție de natura fizică a fenomenului de îndoire putem spune că axa grinzi curbe continue trebuie să fie continuă și netedă (cei care nu au pauze) curba. Deformarea unei porțiuni a fasciculului este determinată de curbura curbei sale elastice, adică curbura axei fasciculului.

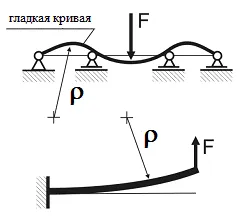
Anterior am formulă pentru determinarea curburii lemnului (1 / ρ) a fost obținută la încovoiere

.

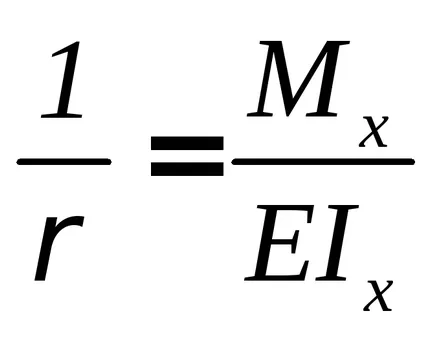
Pe de altă parte, matematică desigur superior este cunoscut faptul că ecuația planului de curbură a curbei este după cum urmează:

.

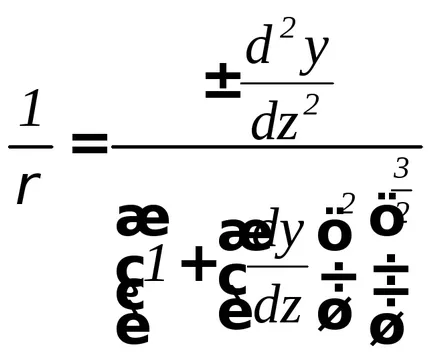
Prin echivalarea cea din dreapta a acestor expresii, obținem ecuația diferențială a axei îndoite a fasciculului, numită ecuația exactă axei fasciculului curbe

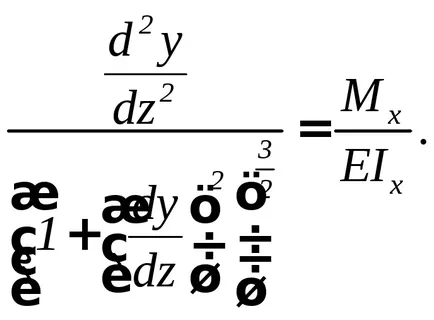
În sistemul de coordonate al z0y jgheaburi. când axa y este îndreptată în sus, semnul determină semnul timpului al doilea derivat al lui y de z.

Integrarea acestei ecuații este, evident, prezintă unele dificultăți. Prin urmare, este de obicei scrisă într-o formă simplificată, indiferent de valoarea în paranteze în ceea ce privește unitatea.

Apoi, ecuația diferențială a liniei elastice a grinzii vor fi luate în considerare în forma:

Soluția ecuației diferențiale (6.1), vom găsi, prin integrarea ambelor părți asupra variabilei z:

Integrarea Constantele C1. D1 este găsit de condițiile limită - condiții fasciculului de fixare, grinzile vor fi determinate prin constanta lor pentru fiecare parcelă.

Luați în considerare procedura de decizie de date pentru un exemplu specific de ecuații.

Lungimea fasciculului consolă l. încărcat cu o forță transversală F. Material fascicul (E), forma și mărimea secțiunii sale (Ix), se presupune, de asemenea, să fie cunoscută.

oh

în cadrul legii schimbării unghiului de rotație  (z) și deflexie y (z) a fasciculului de-a lungul lungimii sale și valorile lor la secțiuni specifice.

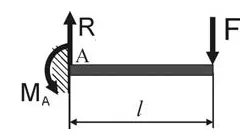
a) să definească zadelke reacție

b) metoda secțiunilor definesc un moment de încovoiere internă:

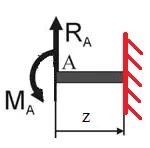
c) determină unghiul de rotație al secțiunilor fasciculului

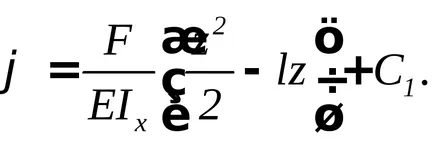
C1 constantă este găsit de condițiile de fixare, și anume - o etanșare strânsă a unghiului de rotație este zero, atunci

Am găsit unghiul de rotație al capătului liber al fasciculului (z = l):

„Minus“ semn indică faptul că secțiunea sa transformat sensul acelor de ceasornic.

d) să definească deformarea fasciculului:

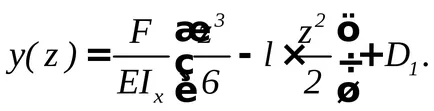
D1 Constant este găsit de condițiile de fixare, și anume - o etanșare etanșă a deformării este zero, atunci

Găsim deformarea capătului liber al fasciculului (x = l)

.

„Minus“ semn indică faptul că secțiunea transversală a căzut jos.

6.3. Ecuația universală a liniei elastice. Method parametrii inițiali

Folosind tehnica descrisă pentru determinarea deplasării grinzilor având mai multe secțiuni, este destul de consumatoare de timp, deoarece pentru n număr de porțiuni constante arbitrare (C și D) crește la 2n. Pentru a reduce activitatea de calcul, în astfel de cazuri, a dezvoltat o serie de metode, inclusiv metoda parametrilor inițiali, permițând orice număr de site-uri pentru a reduce soluția la găsirea doar două constante - deformarea și unghiul de rotație la origine.

D

Pentru a pune în aplicare metoda parametrilor inițiali este necesară pregătirea ecuației momentelor de domenii și integrarea acestei ecuații următoarele reguli:

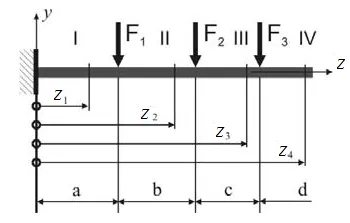
1) originea coordonatelor trebuie selectate comune pentru toate site-urile din punctul cel mai din stânga grinzii;

2

) Toate componentele ecuației momentelor din secțiunea anterioară trebuie menținută neschimbată în ecuația momentelor ulterioare secțiuni;

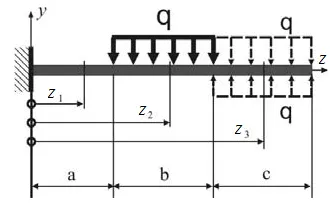
3) în cazul unei întreruperi de sarcină distribuită le extinde la capătul grinzii și pentru a restabili condițiile de încărcare reale administrate „compensare“ de încărcare inversă

4) Integrarea ecuației de la toate site-urile nu ar trebui să dezvăluie paranteze.

P

Să considerăm un segment al unui fascicul de încărcat printr-un sistem arbitrar de forțe și momente (reacții de sprijin, de asemenea, prezente ca și forțe externe), și să facă pentru ecuații ei moment arbitrar secțiune transversală, în conformitate cu aceste reguli:

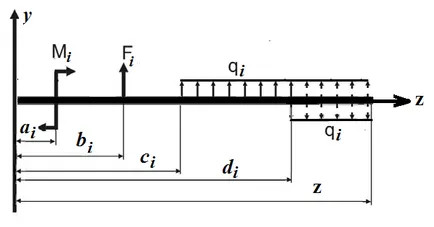
PostoyannyeDi (i = 1, 2, 3, 4, 5) trebuie selectată astfel încât secțiunea transversală a tranziției balkiypri funcția de deviere de la secțiunea secțiunii este continuă. În cazul în care următoarele condiții:

Aplicarea principiului superpoziției, vom scrie ecuația universală a axei îndoite a fasciculului în forma sa cea mai generală:

Diferențierea (6.7) obținem ecuația pentru determinarea unghiurilor de rotație:

Metoda de determinare a deformării și unghiurile de rotație ale grinzii pe baza formulelor (6,7-6,8) se numește metoda parametrilor inițiali.

Rețineți că soluția problemelor este convenabil pentru a scrie ecuația prima pentru cel mai îndepărtat universal de pe site-ul de origine, atunci ecuația pentru secțiunile anterioare cu ușurință, izbitoare din condițiile rezultate ale ecuației, luând în considerare sarcina pe secțiunile următoare.

Odnoprolotnaya consola fasciculului este sub influența unei nagruzkiq distribuite (fig. 6.3). Găsiți ecuație diferențială de îndoire și de a găsi deturnări și unghiurile de rotație la grinzi jumătatea deschiderii și la sfârșitul porțiunii sale braț de parametrii inițiali.

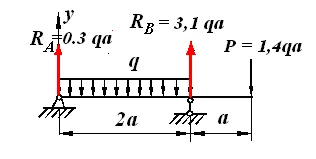
Noi formează ecuația de echilibru:

Pentru a verifica dacă valoarea de răspuns găsită este a treia ecuație - suma proiecțiilor pe axa y verticală:

Prin urmare, reacția găsit adevărat.

Pentru a calcula deformarea fasciculului folosind ecuația universală de sarcină distribuită ar trebui să ajungă la capătul din dreapta al fasciculului. Prin urmare, distribuite de încărcare ING continuă la secțiunea de raportare și adăugarea la fel, dar direcția opusă (Figura 6.4). Adăugarea aceeași sarcină ca rezultat al unei tulpini care este echivalent cu zero static, care nu cauzează schimbări în starea deformată a fasciculului.

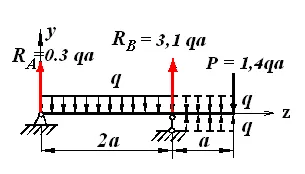
Scriem ecuația universală:

Pe grinzile de susținere la z = 0, z = 2a au y = 0.

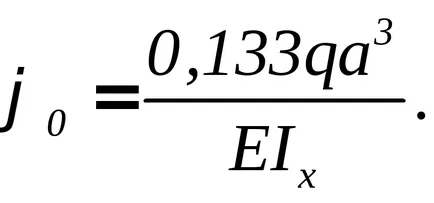
Astfel, ecuația universală devine:

Pentru determinarea unghiurilor de rotație de-a lungul lungimii secțiunilor de fascicul diferenția această ecuație:

Definiți devierilor în mijlocul deschiderii fasciculului, iar la sfârșitul secțiunii sale de braț.

;

Acum definim unghiurile de rotație ale secțiunilor: