Definirea moment de inerție prin trifilyarnogo suspensie

Determinarea momentului de inerție al corpului

de trifilyarnogo suspensie

Numele și inițialele Grupa _____________ ______ ______ Data

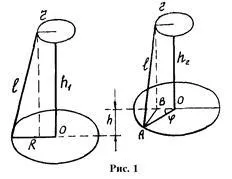
Momentele de inerție ale diferitelor corpuri pot fi măsurate prin oscilațiile torsionale folosind o suspensie așa-numita trifilyarnogo. Trifilyarny suspensie formată din masa m disc și R. raza suspendată pe trei filamente metalice dispuse simetric. Deasupra acestor filamente sunt fixate simetric pe marginile discului de mai mică rază r (Fig. 1).

Când discul D1 este rotită cu un unghi mic în jurul unei axe verticale perpendiculare pe planul discului și care trece prin centrul său, cele trei fire să ia o poziție înclinată, centrul de greutate este ridicat oarecum pe axa de rotație a înălțimii h. Eliberarea discului, ea începe să se efectueze oscilații torsionale a căror perioadă va depinde de momentul de inerție al sistemului. Când ridicați discul la o înălțime h este incrementat energie potențială # 916; Wn = mgh. Cu trecerea discului, prin poziția de echilibru, energia potențială este transformată în energie cinetică a mișcării de rotație.

Neglijarea de frecare, putem scrie

Viteza unghiulară a discului poate fi găsit prin luarea derivatului de deplasare unghiulară # 966;. .

Din moment. atunci. atunci

Vom găsi valoarea h. Considerând că h1 + h2 ≈ 2 # 8467;

Fig. 1 care h1 ² = # 8467; ² - (R - r) ² și

Substituind valorile h1 ² ² și h2 în (3), obținem

Datorită micimea unghiului # 966; sine a acestui unghi poate fi înlocuită cu valoarea sa (# 966;).

Luând în considerare acest lucru, putem scrie:

Substituind (4) și (2) în formula (1), în cele din urmă am obține

Ordinea de performanță

2. D1 # 961 Cunoscând densitatea materialului discului; = 7,8 # 903; 10³ kg / m³, se calculează greutatea sa

3. Adu să oscileze D1 disc. Se măsoară timpul de 50 de oscilații complete și calculează perioada de oscilație a discului neîncărcată

4. Conform formulei (5) pentru a calcula momentul discului inerție I0.

5. Se determină m1 în greutate. care este necesară pentru a determina momentul de inerție.

6. Puneți corpul de masă m1 pe disc, astfel încât sarcina distribuită uniform, pe trei fir, și pentru a determina perioada de oscilație T1. corp disc sistem, și momentul de inerție I1 calculat prin formula (5).

7. Determinarea momentului de inerție a corpului Ix. știind că

8. Toate datele înregistrate în tabel

1. Ceea ce se numește fluctuații?

2. Care sunt numite oscilații armonice?

3. Ce se spune amplitudine, faza, faza inițială, o perioadă a frecvenței de oscilație ciclică?

4. Figura oscilații armonice. Cifra arată amplitudinea, perioada, o fază inițială.

5. Ecuația record arc oscilant.

6. Care sunt viteza și accelerația punctelor vibratoare.

7. Care sunt numite oscilații libere?

8. Ce forțe sunt numite cvasi-elastice? Prin ce forțează vibrațiile corpului apar în lucrare?

9. oscilatii armonice construi Picture derivate de legea x = cos A0 + A1 (# 969; t + f0) /

10. Ia-o imagine de oscilație care rezultă în adăugarea a două oscilații reciproc perpendiculare, în cazul în care diferența de fază este 0.

11. Cum se schimba frecvența naturală a oscilând cu creșterea greutății corporale de două ori?

12. Care este energia totală a vibrațiilor care au loc conform legii x = A0 + A1 Cos (# 969; t + f0)?