Cum să atragă locul radacinilor pentru sistemul

Sistemul de feedback devine stabil atunci când rădăcinile ecuației ce descriu sistemul sunt supuse unei anumite scheme. În caz contrar, sistemul devine instabil. Un exemplu de un astfel de sistem instabil este un microfon, care emite un sunet de perforare. Unele dintre sunetul de la difuzor înapoi în microfon și amplificat de un amplificator, și apoi se duce la dinamica și re-intră microfonul și din nou și din nou, merge într-un cerc, în timp ce amplificatoarele nu intră în modul de saturație și încep să producă zgomot de înaltă frecvență ascuțite. Feedback păstrează uneori sistemul pe marginea de instabilitate și conduce la faptul că sistemul începe să oscileze. Acest efect poate fi util în electronică și alte domenii în cazul în care aveți nevoie de o oscilație de echilibru; în dispozitive, cum ar fi ceasuri. Dar dacă granițele au fost proiectate nu tocmai mica schimbare poate avea rezultate dezastruoase. Acest efect a distrus unele poduri, așa cum au început să oscileze și aceste oscilații sunt de sub control, ca oameni, mașini sau trenuri care trec pe aceste poduri. Recent construit Londra Podul deschis pietonilor pe mileniu, era aproape de o astfel de distrugere în ziua deschiderii sale, dar din moment ce el era încă sub supravegherea atentă a designerilor, a fost închis, iar în caz de catastrofe a fost evitată. Root Locus ajută inginerii pentru a obține o descriere detaliată a sistemului lor, în scopul de a atinge criteriul de stabilitate. Și, în timp ce toate software-ul Academiei aglomerat pentru imaginea „locus rădăcină“, el este încă foarte atractivă pentru toți inginerii - cercetători care doresc să înțeleagă această metodă, și cum să construiască această imagine.

paşi de editare

Edit Metoda 1 din 2:
preliminarii

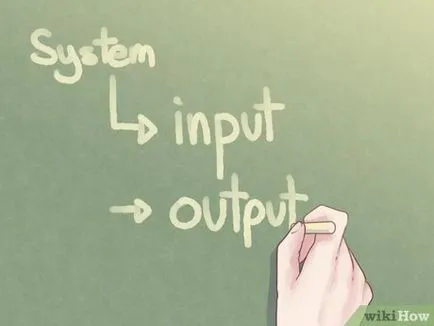
Amintiți-vă că există o foarte simplu de intrare și de ieșire a sistemului. Intre ele este sistemul. Sistemul primește semnalul de intrare, atunci acesta este convertit și iese ca semnal de iesire dorit. Sistemul este construit astfel încât să se creeze conversia dorită pentru a obține un semnal de ieșire.

Noi reprezentăm sistemul într-o cutie. Semnalul de intrare intră sub formă de săgeți și de ieșire din acestea emană în formă de săgeată.

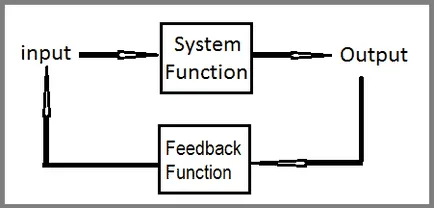
• Acțiunea pe care sistemul efectuează pe semnalul de intrare, numit o funcție a sistemului.

Înainte de a se angajeze la acest lucru, sistemul efectuează întotdeauna pe semnalul de intrare unul din cele trei lucruri,

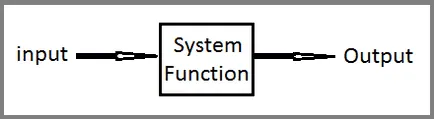
• Această rădăcină se numește locus rădăcină complot polar 180 °.
• slăbire simplă această intrare. În acest caz, se spune că câștigul este mai mică decât unitatea (0
• Doar păstrați-l valoare. In acest caz, se spune că factorul de amplificare este egală cu unu (K = 1).
• Doar crește. În acest caz, se spune că câștigul este mai mare decât unu (K> 1).

Înainte de a introduce această caracteristică, sistemul poate inversa de intrare, rotiți-l și apoi ea face din el unul din cele trei lucruri,

• Acest locus rădăcină se numește locus rădăcină de 0 °.
• slăbire simplă această intrare. În acest caz, se spune că factorul de amplificare este mai mare decât un minus (-1
• Doar păstrați-l valoare. În acest caz, se spune că câștigul este un minus (K = -1).
• Doar crește. În acest caz, se spune că factorul de amplificare este mai mică de un minus (K> 1).

K este câștigul de sistem.

Sistemul de buclă închisă este calea de ieșire la intrare și ieșire din spate și este conectat la intrarea.

Creșterea '' K> 1/4 ''. Discriminantul este negativ. Vei avea două rădăcini complexe conjugate imaginare. Dar valoarea reală a ambelor rădăcinile rămân aceleași și va fi egală cu „“ 1/2 „“. O creștere suplimentară a „“ K „“, fie ca nu afectează numai partea imaginară va crește. Root locus reprezentat prin linii groase.

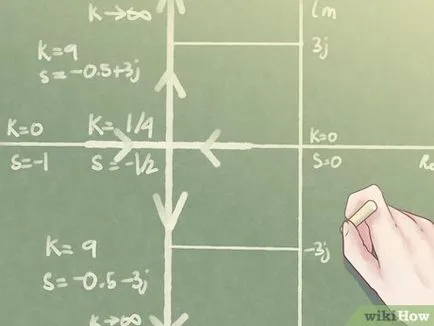
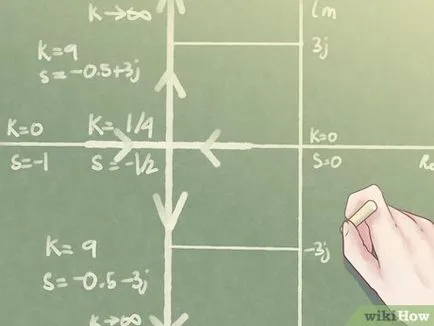
• Pentru aceasta există două rădăcină pătrată a polinomului, și tocmai acestea sunt unite într-un singur punct de pe axa numerelor reale, pentru o anumită valoare a parametrului „K“, în care discriminante devine zero și rădăcinile sunt egale.
• O parte a axei reale între cele două rădăcini - o parte din locus rădăcină.
• Această parte se numește „“ σ-punct „sau“ punct de ramificare „locus asimptota rădăcină.
• Până la această valoare, „K“ este un sistem de amortizare, fără abateri (nu vibreze înainte de oprire).
• Când „= K 1/4“ sistem „“ drastic atenuat.
• După aceea, o creștere „“ K „“ crește doar partea imaginară a rădăcinilor conjugate.
• Acest lucru face ca ramificarea locus rădăcină perpendicular pe axa reală.
• Teoretic, acest sistem este atenuat peste axa, dar cu variații. În practică, creșterea amplificării poate duce la instabilitatea sistemului. Fluctuațiile poate deveni atât de lungi încât inițiază frecvențe nedorite în sistem, care, la rândul său, va aduce sistemul dincolo de limitele puterii sale financiare. De exemplu, mici fisuri ajunge la semne catastrofale sau oboseala dinamică conduce la formularea sa. De aceea, designerii sunt întotdeauna dornici să ia în considerare structura, astfel încât să se prevină o creștere nelimitată în „“ K „“.

Vă rugăm să rețineți că planul complex nu arata ca o intindere reala.

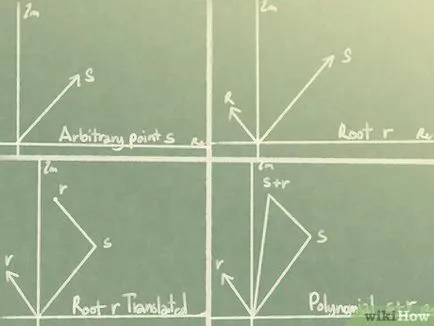
• Pe linia reală, vă sunt limitate la intervale de timp. Pentru a calcula integrala sunt doar cele două numere de capăt.
• Pe planul complex, nu puteți muta oriunde. În schimb, va trebui să selectați o zonă și pentru a limita calculul. Dar chiar și atunci va fi prea mare. Ai nevoie pentru a limita dvs. de calcul anumite curbe sau anumite căi (de obicei simple).

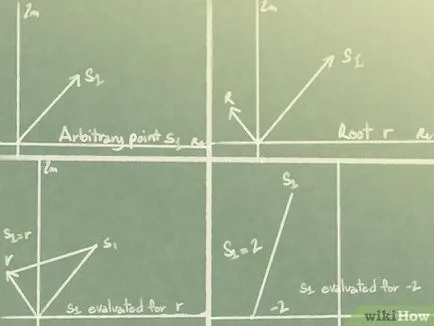
Verificarea Rate punct arbitrar "s" 1 cu polinomul rădăcină "s" "+" "2" "= 0". Acesta este un vector care merge de la vârful „s“ 1 „r“ vertex.

Să presupunem că aveți un anumit număr de rădăcini reale pe linia reală. Trebuie să știi în ce parte a liniei reale este locul radacinilor ca câștig „K“ variază de la zero la infinit plus.

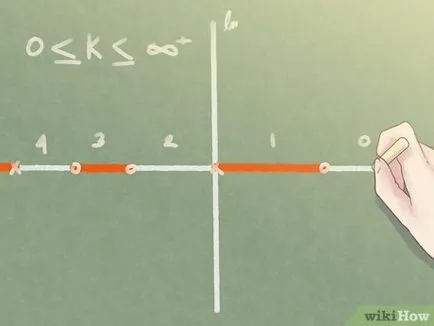
• Selectați orice punct de pe linia reală, în cazul în care numărul de rădăcini reale (zero-uri și stâlpi) sunt dreapta rădăcină - un număr impar (1, 3, 5, ...), atunci acea parte a liniei reale - de asemenea, face parte din locul radacinilor.

Într-o unitate de simplu toate punctele care fac parte din partea negativă a liniei reale, au doar o singură rădăcină de pe partea dreaptă. În consecință, toate linia reală negativă se află pe locul radacinilor.

Dispozitivul de control la numai aceste puncte, linia reală între „s“ = 0 „și“ s „= - 1“ au un număr impar de zerouri în partea dreaptă. În consecință, numai porțiunea dintre „s“ = 0 „și“ s „= - 1“ se află pe locul radacinilor.

Rețineți că funcția caracteristică pentru bucla de feedback global a fost "1 + G (" s ") H (" s ") = 0". câștig separată „K“, ori de câte ori el este, ca un parametru separat și înregistrează ecuația caracteristică în formă de „1 + KF (“ s „) = 0“, unde „F (“ s „)“ funcția rațională; adică "F (" s ") = N (" s ") / D (" s ")". Ambele funcții N ( "s") "și" D ( "s") „polinoame.

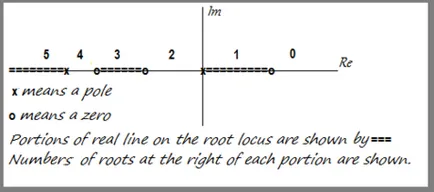
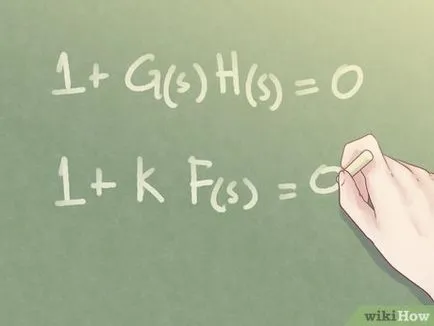
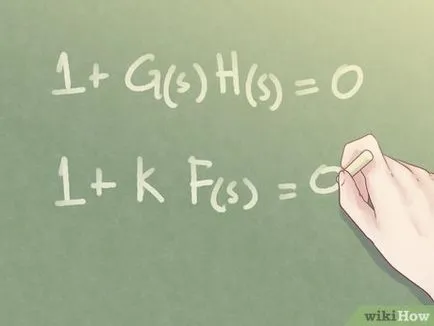
• Roots "N (e)", adică zerouri "F (" s ")" polinoame de gradul I "m".
• Roots "D (e)", adică, polii "F (" s ") sunt polinoame de gradul I" n“.
• Funcția caracteristică pentru o unitate simplă are forma „1 + K /“ s „= 0“.
  • "F (" s ") = 1 /" s "".
• Funcția caracteristică a sistemului de control al motorului are forma 1 + K / s (1 + s) = 0.
  • F (s) = 1 / s (1 + s).

Definirea sistemului „realizabil fizic“. Sistemul realizabil fizic, „m“ "<“ “n”. количество нулей строго меньше количества полюсов. То есть, система не возвращается назад или не допускает бесконечных переходов.

Înțelege sensul ramurilor. Ramurile - un mod de a crea rădăcinile funcției caracteristice, atunci când valoarea câștigului „K“ variază de la zero la infinit. Fiecare valoare de „K“ produce o nouă funcție caracteristică cu rădăcini diferite.

• Dacă doriți să dea „la“ noua valoare în ecuația polinomul caracteristic și pentru a rezolva pentru a obține rădăcini, va trebui să utilizați un calculator sau o metodă grafică, cum ar fi locul radacinilor pentru a descrie soluții.