Criteriul Nyquist - studopediya

Criteriul de stabilitate Nyquist este formulată și validată în 1932 de fizicianul american H. Nyquist. Criteriul Nyquist de stabilitate este utilizat pe scară largă în cea mai practică de inginerie din următoarele motive:

- stabilitatea sistemului într-o stare închisă, prin explorarea funcției sale de transfer de frecvență a părții deschise a Wp (JW), iar această funcție este cel mai adesea este format din factori simpli. Coeficienții sunt parametrii reali ai unui sistem care vă permite să le selectați din condițiile de stabilitate;

- pentru a investiga stabilitatea poate utiliza caracteristicile obținute experimental frecvență a elementelor mai complexe ale sistemului (organele de executare obiect de control), ceea ce mărește acuratețea rezultatelor;

- stabilitatea sistemului poate fi studiat pe o caracteristici de frecvență logaritmice, a căror construcție nu este dificil;

- pur și simplu, rezervele de stabilitate a sistemului definit;

- Este util pentru evaluarea durabilității SAR cu întârziere.

Criteriul de stabilitate Nyquist face posibilă evaluarea stabilității APFC SAR partea sa deschisă. În acest caz, există trei cazuri de aplicare a criteriului Nyquist.

porțiunea 1.Razomknutaya stabilitate ATS ustoychiva.Dlya a unui sistem închis este necesar și suficient ca APFC parte deschisă a sistemului (complot polar Nyquist) cu frecvență w 0 până la + ¥ punct care nu sunt acoperite cu coordonatele [-1, j 0]. Fig. 4.6 prezintă situațiile principale:

1 - sistem închis este absolut stabil;

2. - ATS stabilă condiționat, adică este stabilă numai într-un anumit interval de variație a coeficientului de transmisie k;

3. - ATS este la granița durabilității;

4. - PAC instabilă.

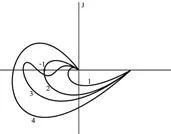
Fig. 4.6. Hodographs Nyquist, atunci când porțiunea de buclă deschisă a SAR este stabilă

2. O porțiune deschisă este la granița ATS ustoychivosti.V acest caz, ecuația caracteristică este zero sau pur rădăcini imaginare și rădăcinile părților reale negativ rămase.

Pentru stabilitatea sistemului închis. Dacă nu există nici o parte a sistemului este la limita de stabilitate este necesar și suficient ca APFC parte deschisă a sistemului atunci când se trece de la 0 la w + ¥, completată cu zona de discontinuitate este infinit de mare raza arcului nu este acoperit punct cu coordonatele [-1, j 0]. În prezența # 957; APFC deschide la zero rădăcini ale sistemului atunci când w = 0 la infinit mari mișcări raza arcului de axa reală pozitivă la un unghi de grade în sens orar așa cum se arată în Fig. 4.7.

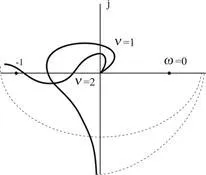
Fig. 4.7. Hodographs Nyquist în prezența la zero rădăcini

Dacă există o pereche de pur imaginare = rădăcini wi. APFC la wi frecvență infinit de mare arc raza trece printr-un unghi de 180 ° în sensul acelor de ceasornic, așa cum se arată în Fig. 4.8.

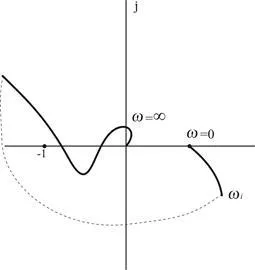
Fig. 4.8. Izvor de falie Nyquist în prezența unei perechi de rădăcini imaginare

3. Deschideți o parte a sistemului este instabil. și anume l Ecuația caracteristică are rădăcini cu partea reală pozitivă. În acest caz, pentru stabilitatea unui sistem închis este necesar și suficient ca frecvența este variat de la 0 la w + ¥ APFC porțiune deschisă acoperit punctul ATS

[-1, j 0) l / 2 ori în direcția pozitivă (invers acelor de ceasornic).

Atunci când o formă complexă a locusului Nyquist este mai convenabil de a utiliza o formulare diferită a criteriului Nyquist propus Ya.Z. Tsypkin utilizând regulile de tranziție. Lumina zilei APFC parte deschisă a sistemului prin creșterea intervalului w al axei reale de la -1 la - ¥ descendentă considerate pozitive (. Figura 4.9), și de jos în sus negativ. Dacă APFC începe la un anumit interval de timp, când w = 0 și se termină la w = ¥. se consideră că APFC face podeaua de tranziție.

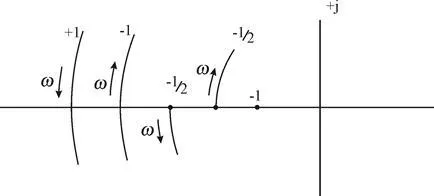
Fig. 4.9. Treceri locus Nyquist prin segmentul P (w) de pe - ¥ la -1

Un sistem închis este stabil dacă diferența dintre numărul de tranziții pozitive și negative locusul prin intervalul Nyquist pe axa reală de la -1 la - ¥ egal cu l / 2 unde l - numărul rădăcinilor ecuației caracteristice cu o parte reală pozitivă.