Contorizarea conceptul

grafice planare. Formula lui Euler.

Luați în considerare imaginea graficului G. Figura 34 reprezintă un grafic G, unele margini ale re-se intersecteaza. In figura 35, același grafic G este reprezentat, astfel încât marginile sale să nu se suprapună.
Graficul din figura 40 este o reprezentare plană a graficului din figura 39.

Fig.39 Fig. 40
Un grafic G este planar dacă poate fi tras într-un plan plat, astfel încât două din coastele lui nu au avut alte puncte în comun, în afară de vârful lor comun.
Exemple de grafice plane sunt cicluri simple, copaci, pădure.
Deoarece caracteristicile unei reprezentări plate a graficului TSB-noțiunea de față.
Edge într-o reprezentare plană a unui grafic G este o parte a planului delimitat de un ciclu simplu și care nu sunt conținute în celelalte cicluri.
Deoarece fețele pot fi considerate ca făcând parte din poziția curse plane „în afara“ reprezentarea plană a graficului; este limitată la ciclul simplu „interior“ și nu conține alte cicluri. Această parte a planului se numește fața „infinit“.

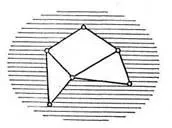
Fig. 41
În figura 41 o parte din fețele umbrite fără sfârșit.
Lemn și lemn au un aspect al infinitului.

Fig. 42
Sarcina 7.1. În Figura 42 o reprezentare plană a unui grafic G. Dă-i margine.
Răspuns: (1, 7, 4, 1), (1, 3, 2, 4, 1), (1, 2, 3, 1), (2, 6, 5, 4, 2), (1, 2 , 6, 5, 4, 7, 1).
De ce parte-OEP-plan delimitat de un ciclu simplu (1, 2, 4, 1) nu este margine etsya?
Deoarece cuprinde ciclul (1, 2, 3, 1).
Sarcina 7.2.

Fig. 43
Care sunt toate fațetele graficului.
Răspuns: (1, 2, 3, 4), (1, 2, 3, 4, 5, 1).
De ce este o parte a planului delimitat de un ciclu simplu (1, 2, 3, 4, 5, 1), este o față?
Deoarece muchia (4, 5), situate în interiorul feței nu formează o buclă.
Sarcina 7.3.

Fig. 44
Este o parte a planului, zashtri Hove în Figura 44 marginea?
Raspuns: Nu, pentru că nu este un căpcăun-nichena în interiorul unui ciclu simplu.
Sarcina 7.1.
Municipalitatea a decis să construiască în fiecare sfert din oraș, având 155
intersecții și segmente de stradă 260 între intersecții, supermarket.
Cât de mulți vor fi construite supermarket-uri?
Decizie.
Harta orașului poate fi considerat grafic planar G, în care intersecțiile sunt noduri și segmente de stradă - coaste.
grafic planar prezentat în Fig. 45 are trei fațete, în care fateta 1 - în afara și fețele 2 și 3 - Intern.

Figura 45
Teorema 10. Formula lui Euler. Pentru fiecare ecuație graf planar conectat este adevărată: n-m + f = 2, numărul gden- număr vershinm- de margini, AF- numărul de muchii de grafice.
Dovada.
Subgraf al G, care conține toate nodurile graficului se numește Spanning. Dacă ostavny subgrafic este un copac, este numit un arbore de acoperire.
Să considerăm un arbore de acoperire Tgrafa G. Este clar că graficul Timeet n vârfuri și o față (exterior). Deoarece T - un copac, numărul de muchii este egal cu T (n-1). Prin urmare, pentru contele Tdokazyvaemaya formulă este adevărată. Acum va pe rând, dar pentru a adăuga lipsă marginile T ale lui G. Atunci când fiecare număr adăugarea de noduri acțiuni de verificare și numărul de muchii și se confruntă cu creșteri pe unitatea de-nitsu. Acest lucru înseamnă că formula va fi dovedită adevărată pentru orice grafic obținut prin adăugarea operațiunilor de coaste, și, prin urmare, pentru graficul inițial. Acest lucru dovedește teorema.
Din moment ce sferturi oraș corespund fețele interioare ale unui grafic planar G, vom găsi numărul de chipuri în formula lui Euler. Un grafic G are 155 de noduri și 260 de margini. Numărul de fețe în ea: f = m - n + 2 = 260 - 155 + 2 = 107.
În oraș pentru a construi 106 supermarketuri.
Sarcina 7.2.
Placa de circuit imprimat este o placă de material, în care prize fabricate special montate instrumente electronice izolatoare. Deoarece conductorii de legătură aceste dispozitive sunt bolborosi piese metalice. Deoarece conductorii nu sunt izolate, piesa nu trebuie să fie trecut. Ec-în cazul în care se poate întâmpla, că una dintre pistele sunt transferate la alte bord o sută de lei. Designer Ivanov a venit cu un bun sistem de o placă de circuit imprimat, care este format din 12 dispozitive și 32 de sârmă, conectați-ing-le. Este posibil să se facă o astfel de taxă, astfel încât toate firele sunt dispuse pe o parte?
Decizie.
Circuit PCB poate fi reprezentat ca un grafic, ale cărui noduri vor reprezenta dispozitive de autobuz, și marginile - fire conectarea acestora. Soluția de rezolvare a problemei se reduce la a răspunde la întrebarea: Va graful G, înfățișând inginerului la lui Ivanov plat?
Să demonstrăm următoarea relație: Propoziția 3: pentru un apartament foie-fa conectat, soderzhaschegonvershin imreber, pentru N. 3 executat inegalitate stvom. 3n- 6.
Dovada. Să G1, G2, ..., pragul Ff- a graficului G, și m1, m2. mf- este limitarea numărului de muchii, respectiv, fiecare față. Găsiți suma S = m1 + m2 +. + Mf.
Deoarece fiecare față a graficului delimitat de cel puțin trei coaste, The 3f. S. Pe de altă parte, fiecare margine aparține sau două fețe sau fețe, adică, în cantitate de S este luată în considerare de două ori sau de unul. De aceea, S. 2m. Trebuie să 3f. 2m. În continuare, vom folosi formula lui Euler:
f = m - n + 2,
3f = 3m - 3n + 6
2m? 3m - 3n + 6,
m. 3n - 6.
Pentru n = 3neravenstvo verificat direct.
Inegalitatea este dovedit.
Pentru graful G, descriind inginerul de la Ivanova, n = 12, m = 32, iar inegalitatea de mai sus nu este îndeplinită.
Prin urmare, Gne grafic este plat și de a face taxa de nyuyu o singură față imposibilă.
Sarcina 7.3.
Inginer Ivanov (cm. Problema anterioară) îmbunătățit costul său. Acum are dispozitive 9 și 17 din conductorii (vezi placa de circuite. Fig. 46). Este posibil să se facă bord, astfel încât toți conductorii burghers-timp pe de o parte?

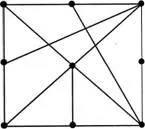
Figura 46.
Decizie.
Presupunem circuitul grafic bord G. Inegalitatea m. 3n - 6 nu poate răspunde dacă un grafic G plat ca 17. * 3 9 - 6 = 21.
Să considerăm subgraful lui G, linii îngroșate în figura 47.

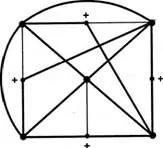
Fig. 47
Acest subgrafic poate fi obținut din grafic complet cu cinci noduri (C5) plasarea pe unele-ryh coaste noduri suplimentare. (Noduri Figura K5vydeleny și vârfuri suplimentare sunt etichetate semnul „+“). Intro-de vârfuri suplimentare nu pot converti neplană grafic K5 în apartament. Prin urmare, graficul G, a cărui subgrafic este un grafic neplană este, de asemenea, non-planară. Acest lucru înseamnă că, pentru a produce-o parte a plăcii imposibilă.
Teorema cunoscută descrie structura graficelor planare. Împărțim unele dintre marginile grafice și noduri K3,3 K5novymi (vezi. Fig. 48). Graficele rezultate vor fi numite, respectiv, grafice tip K3,3 și K5.

Teorema 11.TeoremaPontryagina-Kuratowski (1927.1930 g). Graficul este plat dacă și numai dacă acesta nu conține subgrafurilor tipuri K3,3 sau K5.