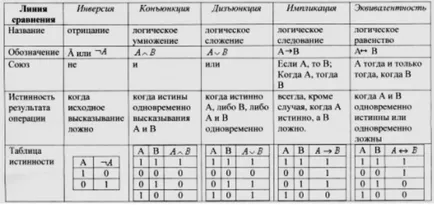
Construirea de tabele de adevăr

Prioritate în punerea în aplicare a operațiunilor ordinului sunt paranteze.

Un algoritm pentru construirea unei funcții de adevăr tabelă logică

Se determină numărul de rânduri: Număr rânduri = $ 2 ^ n + 1 $ (linie de antet). $ N $ - numărul de expresii simple. De exemplu, există o combinație $ $ 2 ^ 2 = 4 seturi de valori ale variabilelor pentru funcțiile de trei variabile pentru funcțiile de două variabile - $ 2 ^ 3 = 8 $ etc.

Se determină numărul de coloane: Număr de coloane = numărul de variabile + număr de operații logice. La determinarea numărului de operații logice, de asemenea, să ia în considerare ordinea de execuție a acestora.

coloane umplute efectua operații logice rezultate într-o anumită secvență de tabel de adevăr al operațiilor logice de bază.

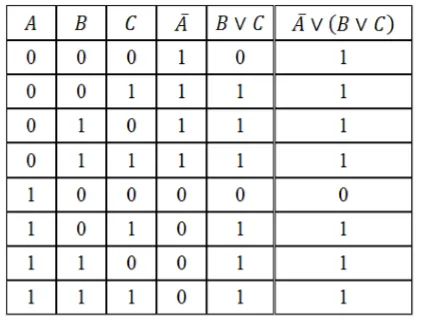
Crearea unui tabel al expresiei logice este adevărat $ D = \ bar \ vee (B \ vee C) $.

Se determină numărul de rânduri:

Numărul de expresii comune - $ n = 3 $, atunci

număr de rânduri = $ 2 ^ 3 + 1 = 9 $.

Definim numărul de coloane:

Numărul de variabile - $ 3 $.

Numărul de operații logice și succesiunea lor:

1. Inversion ($ \ bar $);
2. disjuncție, pentru că este în paranteze ($ B \ vee C $);

disjuncție ($ \ overline \ vee \ stânga (B \ vee C \ dreapta) $) - dorită expresie logică.

Numărul de coloane = $ 3 + 3 = 6 $.

Completați în tabel, având în vedere tabelul de adevăr al operațiilor logice.

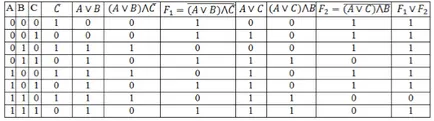
Se determină numărul de rânduri:

Numărul de expresii comune - $ n = 3 $, atunci

număr de rânduri = $ 2 ^ 3 + 1 = 9 $.

Definim numărul de coloane:

Numărul de variabile - $ 3 $.

Numărul de operații logice și succesiunea lor:

1. negare ($ \ bar $);
2. disjuncție, pentru că este în paranteze ($ A \ vee B $);
3. conjuncția ($ (A \ vee B) \ bigwedge \ overline $);
4. negare, pe care vom nota $ F_1 $ ($ \ overline> $);
5. disjuncție ($ A \ vee C $);
6. conjuncție ($ (A \ vee C) \ bigwedge B $);
7. negare, pe care vom nota $ F_2 $ ($ \ overline $);

Număr de coloane = 3 + $ 11 = Indicator $ 8.

Completați în tabel, având în vedere tabelul de adevăr al operațiilor logice.

Un algoritm pentru construirea funcției logice prin tabela de adevăr

1. Alocați un rând de tabel de adevăr cu valoarea funcției egală cu $ 1 $.
2. Scrieți formula dorită ca o pluralitate de disjuncție logică a expresiilor. Valoarea acestor expresii este egal cu numărul de rânduri selectate.
3. Fiecare expresie logică în această disjuncție scrisă ca o conjugare a argumentelor funcției.
4. În cazul în care valoarea unora dintre argumentele funcționale în linia corespunzătoare a tabelului este setat la $ 0 $, atunci acest argument este scris sub forma negația.

Rezolvarea controlului în toate subiectele. 10 ani de experiență! Preț de la 100 de ruble. Perioada de la 1 zi!