condiţii de stringență

rigiditate Starea tijei

O` (rulează unghi ÎNCHIS.) = Mkrmax / G * JRO<[O]

Criterii de ductilitate si fracturi. Prima, a doua, a treia și a patra teorie putere. Toriu Mora. Informații generale despre diferitele ipoteze de rezistență și ductilitate. Soluțiile generale ale planului pentru a testa puterea de a problemei.

In general, o stare periculoasă de stres a elementului structural depinde de relația dintre cele trei tensiuni principale (s1, s2, s3). Ie Strict vorbind, fiecare raport trebuie să determine experimental valoarea tensiunii maxime, ceea ce este nerealist. Prin urmare, au fost luate aceste metode de calcul al puterii, care ar permite să evalueze severitatea oricărei stări de stres de stres la tracțiune - compresiune. Ele se numesc teoriile de putere (teoria stărilor limitative de stres).

Teoria În primul rând puterea (Teoria maximă normală de stres) Pandantiv stabilit: Pentru orice tensiune. capabil de fractură pentru fragile este, dacă max. standarde. Tensiunea atinge limita pentru dannogomateriala dezavantaj principal: nu iau în considerare două alte stres majore. Confirmate prin experienta doar in tensiune, mai degrabă materiale fragile (sticlă, gips). În prezent, aproape niciodată folosit.

sigma max<сигма пред.(экспиремент на растяжение)

sigma echiv. = Sigma Capitol. <[сигма]доп.

A doua teorie a rezistenței (teoria maximă de deformare relativă): Pentru orice tensiune. CoC-ii descărcare fragil. va dacă max. rel. deformare-e făcut înainte. VAL.

Condiții de descărcare-Ia: epsilon epsilon max = pr.

yc-s rezistență :. σekv = σ1-V (nu) * (σ2 + σ3)<[σ]доп.

Teoria treia putere (Teoria stresului maxim de forfecare): Atunci când orice tensiune. wc-ii plasticitate. biți. În cazul în care se ajunge la maxim înainte de tensiunile de forfecare. tmax stare = tpred. tmax = σ1-σ3 / 2, condiția rezistență: σekvIII = σ1 - σ3≤ [σ]. Principalul dezavantaj - nu ia în considerare impactul s2.

Când stresul avion: sekvIII = £ [s]. Când sy = 0 fi utilizat pe scară largă pentru materialele plastice.

4 Teoria lea a puterii (teoria energetică) În orice caz. capabil să se descarce. ar fi în cazul în care activitatea specifică pentru a schimba forma pentru a ajunge înainte. valori.

Se ia în considerare toate cele trei tensiuni principale.

Utilizate pe scară largă pentru materiale plastice.

Teoria Mora Forța obținută prin cercuri de stres Mohr. Este utilizat în calculul materialelor fragile a căror întindere admisibilă stres [sp] și contracția [SC] nu este același (fier).

Pentru materialele ductile [sp] = teoretic [SC] Mora este convertită în a treia teorie.

Mohr cerc (tensiuni cerc). Coordonatele punctelor cercului în tensiunile normale și de forfecare la diferite locuri. Complotat împotriva axei centrale C s grinzii la un unghi 2a (a> 0, apoi împotriva chas.str.), Găsim punctul D,

coordonatele care: sa, ta. Puteți rezolva grafic probleme directe și inverse.

Soluțiile generale ale planului pentru a testa puterea de a problemei:

condiție Strength verificare (es Pentru materiale fragile 1, 2 teoria puterii și teoria rezistenței Mora; Pentru 3aya materiale ductile și teoria putere a patra)

Definim factor de siguranță valid. (N (RMS).)

Găsim secțiunea periculoasă.

pentru 1 si 2 din teorie. Durabilitate secțiunea periculoasă - o platformă perpendiculară pe prima direcție principală

pentru a treia și a patra teorie. secțiunea periculoase - care funcționează la plozadka. Adevărații eforturilor maxime de forfecare. Iar pentru 4 op.sech - câmp octaedrică, și anume încă înclinat tuturor treia axă.

îndoire Curățați și laterală. tipuri de link-uri de sprijin. definiția reacțiilor controversate. Forțele interne la planul de îndoire și relația dintre ele. Parcele de forțe de forfecare și a momentelor de încovoiere. Diferențiale mezhduq conform, Miq.

Dacă directă sau îndoire oblică în secțiune transversală a actelor de tijă doar un moment de îndoire, respectiv semifabricatul are drept sau oblic la încovoiere pură. În cazul în care secțiunea transversală și acționează ca forță de forfecare, există o îndoire transversală dreaptă sau oblică.

Lansete care se execută în principal, pe o curbă, numită grinzi (utilizate în diverse modele de clădiri, poduri, sub forma unei macarale grinzi clădiri industriale și așa mai departe. D.). Ei au un design simplu, fabricație și de încredere în funcțiune.

sprijin Sharnirno'podvizhnaya. Acest suport este un aparat care permite deplasarea secțiunii de suport paralelă cu planul de sprijin și rotirea acestuia într-un plan vertical în raport cu axa îmbinării cilindrice. Acest dispozitiv nu permite să se miște în direcția conexiunii suprapuse pe verticală. reacție de sprijin VA sharnirno_podvizhnoy este direcționat de-a lungul legăturii de referință.

sprijin Sharnirno'nepodvizhnaya. Acest sprijin nu permite deplasarea secțiunii de suport sau în direcțiile longitudinale sau transversale, dar permite rotirea acestei secțiuni cu privire la balama. Pivotabil rulment fix este un rulment cu două conexiuni, care sunt aplicate în mod convenabil, în direcția axei fasciculului și perpendicular pe axa fasciculului. În sprijinul acestei există două componente ale reacției de suport: HA și VA.

fixare rigidă sau de etanșare. Acest suport nu permite rotirea secțiunilor de susținere și pentru a muta în orice naprav_lenii - această secțiune a impus trei obligațiuni: verticale VA. orizontal pe. susținerea componentelor de reacție și îndoire momentul MA.

Dacă secțiunea fasciculului având o axă verticală, sarcina exterioară și forțele reactive se află într-un plan care coincide cu axa secțiune, budetizgibatsya fasciculului în același plan. Această îndoire se numește plat.

Lăsați planul exterior îndoire sarcină perpendicular pe axa longitudinală a grinzii, atunci fasciculul secțiuni transversale cu o forță de forfecare și momentul încovoietor și forța longitudinală este zero. O astfel de îndoire se numește transversal.

dependences diferențiale între q, M și Q.

tensiuni normale la încovoiere pură - ipoteza secțiunilor plane, axa neutră de determinare stres. Stresul normală maximă la încovoiere, secțiunea modulului, fascicul de echilibru rezistență.

Ipoteze secțiuni plane: secțiune perpendiculară pe axa prăjinii și netedă înainte de deformare rămân aceleași și după aplicarea sarcinii.

Din acțiunea momentului de încovoiere în secțiunea transversală fascicul având o tensiune normală, determinată prin formula

,unde M - momentul de încovoiere în această secțiune;

I - momentul de inerție al secțiunii transversale a fasciculului în raport cu o axă neutră;

y - distanța de la axa neutră la punctul în care sunt determinate tensiunile.

De la (8.1), tensiuni normale în secțiunea transversală a fasciculului în ajustarea liniară, atingând o valoare maximă în punctele cele mai îndepărtate ale stratului neutru.

,unde W - secțiune modul în jurul axei neutre a fasciculului. În ipoteza secțiunilor plane presupunând că în interiorul tijei și tulpina să aibă același caracter ca și pe suprafață. Prin urmare, planul secțiunii și perpendicular pe axa tijei înainte de deformare rămâne plat și normal la axa sa și după deformare. Acesta este sensul ipoteza secțiunilor plane.

Axa neutră - o linie în secțiunea transversală a cotului a fasciculului, la punctele unde efort normal paralel cu axa fasciculului, sunt egale cu zero. Secțiunea axa neutră se împarte în două părți, dintre care unul acționează tensiuni normale de tracțiune, iar în cealaltă - comprimare.

Secțiunea modulul este raportul dintre momentul de inerție la o anumită axă la o distanță față de axa la punctul cel mai îndepărtat al secțiunii transversale

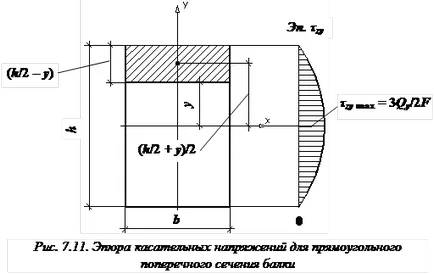
Tensiunea de forfecare în timpul îndoirii. Formula Zhuravsky. Diagrame de tensiuni tangențiale în dreptunghiulară și I-secțiune.

(. Figura 2) efortul de forfecare la orice punct al secțiunii transversale este definită ca stresul pereche produsă în secțiunea longitudinală cu formula Zhuravskoye; Txz =

,unde - forța de forfecare în prezenta secțiune; - momentul static porțiunea tăiată, b - lățimea secțiunii transversale la nivelul punctului, - momentul de inerție al secțiunii transversale întregul în raport cu axa neutră.

Zhuravskoye formulă permite determinarea tensiunilor de forfecare în timpul îndoire, rezultând puncte ale secțiunii transversale a grinzii, la o distanță de axa neutră x. Formula Zhuravskoye pentru forfecare:

,

unde Q - forță transversală; S * x - momentul static fi tăiat o parte din secțiunea transversală în raport cu axa x. F * - zona să fie tăiat o parte a secțiunii transversale, yc - distanța de porțiunea centrală a secțiunii transversale să fie tăiat la axa x. Jx - principala secțiune transversală totală momentul de inerție axial, prin - lățimea secțiunii transversale la punctul pentru care există o tensiune.