Conceptul, sensul geometric și mecanic derivatul său

Lăsați funcția y = f (x) este definit la punctul x0 și un anumit cartier, x - din acest punct cartier. Introducem notația: diferența x - x0 este notat cu # 916; x și apel incrementarea argumentului. iar diferența f (x) - f (x0) este notat cu # 916; y și funcția nazovemprirascheniem.

Astfel, # 916; x = x - x0. # 916; y = f (x) - f (x0). egalității # 916; x = x - x0 obținem
x = x0 + # 916; x, atunci # 916; y = f (x0 + # 916; x) - f (x0).

Derivata funcției f (x) la x0 este limita la raportul funcției increment a creșterii argumentului atunci când incrementul argumentul tinde la zero.

f Derivative denotat „(x0).

Exemplul 1: Găsiți derivata funcției f (x) = x 2 la punctul x0 = 3.

Dacă există f „(X0), atunci spunem că funcția f (x) este diferențiabilă în punctul x0. Vom stabili o legătură între funcțiile derivabile f (x) la x0 și continuitatea sa în acest punct. Să ne amintim că funcția f (x) este continuă în punctul x0, dacă se determină în punctul x0 și o parte din împrejurimile sale și egalitatea următoarele:

Reformulati această definiție, folosind argumentul incrementarea conceptului și funcția increment. Din această ecuație obținem:

Cu alte cuvinte, funcția f (x) este continuă în punctul x0. dacă incrementul infinitezimal a argumentului corespunde unei funcții de creștere infinitezimal.

Teorema. Dacă funcția f (x) este diferențiabilă la x0, IT este continuă în acest punct.

Notă. Dacă funcția punctului x0 f (x) este continuă, atunci în acest moment funcția nu poate fi derivată, după cum reiese din exemplul următor.

Exemplul 2. Funcția f (x) = | x | este continuă în punctul x0 = 0, atunci.
Arătăm că această funcție nu are nici un derivat de la punctul x0.

nu există, de exemplu, f (x) nu este diferențiabilă în punctul x0 = 0.

Să considerăm sensul geometric al derivatului.

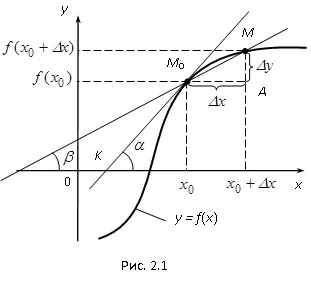
Fig. 2.1 prezintă un grafic al unei funcții continue y = f (x). M0 punct de date are coordonatele X0. f (x0), celălalt punct al graficului M - coordonatele x0 + # 916; x, f (x0 + # 916; x). Direct M0 M este secantă la linia y = f (x), este înclinată față de axa Ox la un unghi # 946;. Fie f „(x0) există, adică, există un anumit număr. din # 916; M0 MA obține (este cunoscut faptul că tg # 946; - panta liniei drepte M0 M). dacă # 916; x → 0, punctul M se deplasează pe graficul funcției y = f (x), se apropie de punctul M0. în care secant M0 M, rotirea în jurul punctului M0. își propune să ia poziția limită, și anume, pentru a coincide cu tangenta M0 K, în timp ce # 946; → # 945; (# 945; - unghiul dintre tangenta și axa M0 K Ox), tg # 946; → tg # 945;.

Astfel, dar tg # 945; = K este panta tangentei M0 K.

Astfel, panta tangentei la curba y = f (x) la x0 cu abscisa este derivata f (x) la x0. f „(x0) = k = tg # 945;.

Aceasta este interpretarea geometrică a derivatului. Evident, ecuația tangentei M0 K este de forma:

Vom continua să ia în considerare derivatul sens mecanic.

Să punctul de masă se deplasează S = f (t), unde t rectiliniu inegal legal - timp, S - calea parcursă în timpul punctului de timp t.

Să presupunem că, în momentul t0 punct a fost în poziția M0 (fig. 2.2). Noi pune problema: pentru a determina viteza punctului material în momentul t0. Luați în considerare un alt punct în timp t0 + # 916; t. Pe parcursul traseului de timp punct t0 este traversat: S0 = f (t0), pentru (t0 + # 916; t) călătorie distanța S = f (t0 + # 916; t), iar punctul a fost în poziția M, apoi pentru timpul # 916; t traseului parcurs M0 M și este egal cu:
S - S0 = f (t0 + # 916; t) - f (t0) = # 916; S.

Viteza medie Vav de timp ppomezhutok # 916; t este egal cu :. Cu toate acestea, rata medie poate fi diferit, în funcție de intervalul de timp # 916; t. Rate la momentul de timp t0 (notat V (t0)) este viteza limită în cazul în care media Vav # 916; t → 0. Astfel,

Concluzie. Derivatul de cale S = f (t) la momentul t0 este viteza la momentul t0 timpului.