Conceptul de factor determinant ordinul n-lea
Determinantul de ordinul n-lea
determinant Determinant sau de ordinul n-lea este numărul care trebuie scris sub forma
și calculat în conformitate cu numerele (reale sau complexe) - elemente determinante
Schema de calcul determinanții ordine de 2 și 3
Fie (delta) este determinantul sistemului matricea A, și (delta) i-determinantul matricei obținută din matricea A prin înlocuirea coloanei j-a chisel.Togda libere coloană dacă (delta) nu este egal cu 0, sistemul este unic determinat în formula:
1.Opredelitel ordinul 2 se calculează cu formula:
2. Factorul determinant al treilea ordin se calculează cu formula:
Există o schemă convenabilă pentru calcularea determinantului al treilea ordin (vezi. Fig. 1 și fig. 2).
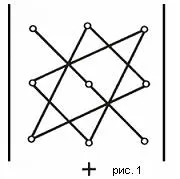
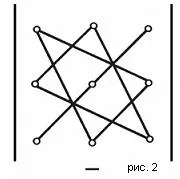
1. Dacă (coloană) matrice rând constă din toate zerouri, atunci determinantul este egal cu 0.
2. În cazul în care toate elementele din orice rând (coloană) a matricei înmulțită cu chilo (lambda) este determinant se înmulțește cu acest număr (lambda).
3. În transpunerea determinantul nu se schimba matricea.
Transpunerea - în matematică, această matrice de transformare coloană-înlocuire pătrat în rând sau vice-versa.
4. La transpunerea două rânduri (coloane) determinantul matricei schimbă semnul.
5. Dacă matricea pătrată cuprinde două rânduri identice (coloana), atunci determinantul este egal cu 0
6. În cazul în care elementele celor două rânduri (coloane) ale matricei sunt proporționale, că factorul determinant este egal cu 0
Produsele 7.Summa de elemente ale unui rând (coloană) elementele de matrice ale cofactori alt rând (coloana) din această matrice este 0
matrice 8.Opredelitel nu se schimbă dacă elementele unei matrici rând (coloană) pentru a adăuga elemente alt rând (coloană), înmulțit anterior cu același număr.
produse 9.Summa din numerele b1, b2. bn adăugării algebrică orice rând elemente (coloană) este egal cu determinantul matricei obținută din aceasta prin înlocuirea elementelor acestui rând (coloana) b1, b2. bn.
produs 10.Opredelitel a două matrici pătrate este produsul determinanților lor | C | = | A | * | B |, unde C = A * B, A și B sunt matrici ordinul n-lea.