clasă de matematică 9 sinus, cosinus, tangenta, cotangentă unghi arbitrar

Să considerăm un cerc cu raza R centrată la originea sistemului cartezian Oxy.

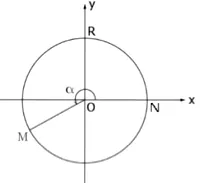
Considerat NOM unghi pozitiv, partea OM se obține din pozitiv jumătate de Boului prin rotație, puse în aplicare în direcția de mișcare invers acelor de ceasornic.

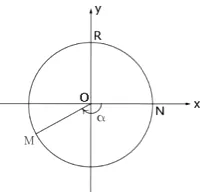
Considerată NOM unghi negativ, partea OM se obține din pozitiv pe jumătate Ox prin rotație, realizată într-o direcție ce coincide cu direcția acelor de ceasornic.

În cazul în care coordonatele punctului M0. situată pe un cerc de rază R, cu centrul la originea O,

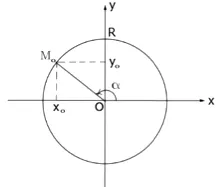
apoi, prin teorema lui Pitagora. Este egalitate:

și poate formula următoarea definiție generală a funcțiilor trigonometrice ale unui unghi arbitrar.

Sinus, cosinus, tangentă și cotangentă unghi arbitrar α numere de apel definite prin formulele:

După cum se poate observa, definiția funcțiilor trigonometrice ale unui unghi arbitrar este o generalizare naturală a definiției funcțiilor trigonometrice unghi ascuțit.

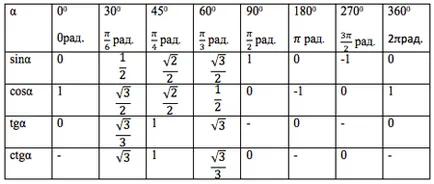
În cele mai multe cazuri, cercul unitate folosită pentru a determina semnul funcției trigonometrice, valori numerice sau tabele sunt calculate folosind calculatorul.

Valorile funcțiilor trigonometrice, trebuie să știi pe de rost.

Întrebări pentru rezumate

Se calculează valoarea expresiei: -sin990º

În cazul în care, apoi se calculează valoarea sinx

În cazul în care, apoi se calculează valoarea TGX