Care este răspunsul la trapezului
Trapez - un patrulater cu două laturi paralele, iar celelalte două nu sunt paralele (figura 1.).
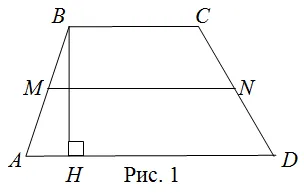
Partea paralelă a trapezului (e) numite baze trapez. în loc de paralele (și) - flancurilor. Perpendicular (), extrase din orice punct o bază la alta baza sau continuarea acesteia se numește înălțimea unui trapez.
trapez proprietate
Suma colțuri adiacente adiacente lateral este egală cu:
Segmentul care leagă mijlocul laturile trapezului, se numește linia de mijloc a trapez. Linia de mijloc paralelă cu bazele trapezului și este egală cu jumătate din suma dintre:
Dintre toate trapezelor pot selecta două clase speciale de trapeze: dreptunghiular și trapez isoscel.
Se numește trapez dreptunghiular în care unul dintre unghiuri este corect.
A numit un trapez echilateral, ale cărui laturi sunt egale.
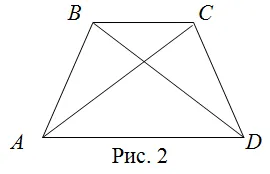
Proprietățile unui trapez echilateral
- Într-un unghi trapez echilateral la perechi de baze sunt egale.
- Diagonalele sunt trapez echilateral egale.
Semne ale unui trapez echilateral
- Dacă unghiurile de la baza trapezului sunt egale, trapez isoscel.
- În cazul în care trapezului diagonalele sunt egale, atunci este isoscel.
în cazul în care - baza trapez, și - înălțimea sa.
Exemple de rezolvare a problemelor
Sarcină. Înălțimea unui trapez echilateral trase din unghiul obtuz, împarte baza de la o lungime de 5 cm și 11 cm. Gasiti perimetrul unui trapez dacă înălțimea este de 12 cm.
Decizie. Vom face desenul (Fig. 3)
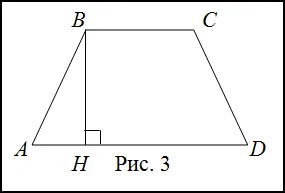
- trapez isoscel, - înălțime, a se vedea, a se vedea, a se vedea.
Să considerăm un dreptunghiular (). Prin teorema lui Pitagora
înlocuind datele originale, obținem
Deoarece trapezului isoscel, laturile sale laterale sunt: cm baza mai mare a trapezului este egală cu :. (Cm). Baza mică a trapezului este egală cu: (cm). Perimetrul trapezului este egal cu:
Sarcină. Cele două părți trapezoizi dreptunghiulare mai mici sunt egale dm 2, și unul din colțuri. Găsiți aria unui trapez.
Decizie. Vom face desenul (Fig. 4)
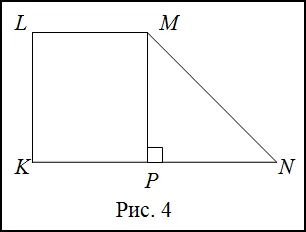
- trapez dreptunghiular, dm ,. picătură înălțimea la baza vârfului. Să considerăm un dreptunghiular (). de atunci
Astfel, de asemenea, și isoscel. În consecință ,. Deoarece dm, în consecință, dm. Baza mai mare, astfel încât să se obțină (dm).
Zona de trapez calculată cu formula:
în cazul nostru va fi:
Substituind valorile cunoscute, obținem