Caracteristicile cantitative și calitative ale informațiilor

Măsurile de informare sunt în general luate în considerare trei aspecte: structurale, STATIS-și-statică semantică.

Aspectul structural, structura matricelor de informații și măsurarea acestora prin simpla numărare elementele de informare sau metode combinatorii. Abordarea structurală este utilizată pentru a evalua capacitățile sistemelor informatice, indiferent de aplicare a acestora.

În abordarea statistică utilizează conceptul de entropie ca o măsură de incertitudine, care ia în considerare probabilitatea de apariție și conținutul informațional al unui mesaj. Abordarea statistică ia în considerare condițiile specifice de utilizare a sistemelor informatice.

Abordarea semantică vă permite să sublinieze utilitatea sau valoarea mesajului de informații.

măsură informațiile structurale

Informațiile sunt prezentate întotdeauna sub forma unui mesaj. Unitate de mesaje elementare - simbol. Caracterele au adunat în grupuri - cuvântul. Mesajul emis sub forma de cuvinte individuale sau caractere, sunt transmise întotdeauna la materialul și forma de energie (,, semnale sonore luminoase electrice).

O informație distincție continuă și discretă (fig. 2.4).

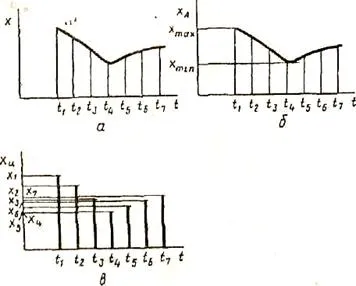
Fig. 2.4. Modalități de prezentare a informațiilor

funcția x (t), prezentat în Fig. Și 2.4. Acesta poate fi reprezentat într-un proces continuu (Fig. 2.4b) și (fig. 2.4) specii discrete. Sub formă continuă a acestei funcții poate lua valori reale într-un anumit interval de variație a argumentului t, adică o multitudine de valori ale unei funcții continue pe termen nedefinit. In forma discretă a funcției x (t) pot primi valori substanță guvernamentală numai pentru anumite valori ale argumentului. Indiferent de interval mic discretă (adică o distanță între valorile de argument adiacente) sau selectează o multitudine de valori discrete ale argumentului funcției pentru un interval predeterminat de schimbare (dacă nu este fără sfârșit) este finită (limitată).

Atunci când se utilizează informații structurale ale măsurilor luate în considerare numai structura discretă a mesajului, numărul conține elemente de informații, conexiunile dintre ele. Într-o abordare structurală, geometrie diferită, combinatorică și aditive măsuri de informare.

măsură geometrică implică măsurarea unui parametru al modelului geometric de posturi izolatoare informaționale (lungime, suprafață, volum) în unități discrete. De exemplu, informațiile geometrice modelul Coy poate fi o linie de unitate de lungime (figura 2.5 și - un singur cuvânt este 0 sau 1), pătrat (Figura 2.5 b. - cuvânt din două cifre) sau un cub (Figura 2.5 în - trei cuvânt cifre). Valoarea maximă posibilă a informațiilor la structuri predeterminate definește informații model de capacitate (sistem), care este definită ca suma valorilor discrete ale tuturor măsurătorilor (coordonatele).

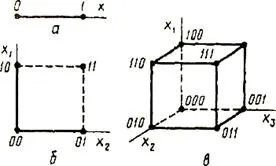
Fig. 2.5.Geometricheskaya informații model de

Informația combinatorie este definită ca numărul de elemente precum numărul de combinații (caractere). Posibila Cantitatea de informații egal cu numărul de combinații posibile și permutări de plasare a elementelor. Combinând simboluri într-un cuvânt constând numai din 0 și 1, schimbând sensul cuvintelor. Luați în considerare două perechi de cuvinte 100110 și 001101, 011101 și 111010. Au avut loc permutare extreme de cifre (a schimbat locația bitul de semn în numărul de - categoria sa mutat de la stânga la dreapta).

măsură Aditiv (măsura Hartley), potrivit căreia cantitatea de date se măsoară în unități binare (biți), cele mai comune. Conceptele de adâncime și lungime.

Adâncimea numărului (q) - numărul de caractere (elemente) luate pentru a reprezenta infor-mațiile. La un moment dat doar unul este realizat un caracter. Numărul de adâncime corespunde sistemului numărul de bază.

Număr Lungime (n) - numărul de posturi necesare și suficiente pentru a reprezenta numere de valoare dată. Lungimea corespunde numărului de biți al sistemului numeric.

Pentru date adâncimea și lungimea numărului de numere care pot fi reprezentate, va
N = q n. Valoarea N este incomod pentru capacitatea de informații de evaluare. Hartley introdus aditiv măsură logaritmică binar, care permite calcularea cantității de informație în unități binare - biți:

Aceasta este unitatea de informații pentru Hartley.

Prin urmare, informațiile de 1 bit corespunde unui eveniment elementar, care pot sau nu pot să apară. Această măsură a cantității de informație este utilă în faptul că acesta oferă posibilitatea de a funcționa ca o măsură a numărului. Cantitatea de informații în care numărul de simboluri binare echivalente cu 0 sau 1. În cazul în care există mai multe surse de informații cantitatea totală de informații

unde (qk) - cantitatea de informații de la sursa k. Măsura logaritmică a informațiilor face posibilă măsurarea cantității de informație și este utilizată în practică.

măsură Informații statistice

Informațiile statistice sunt introduse măsură a valorii teoriei informației, potrivit căreia nu este considerat evenimentul în sine, dar informațiile cu privire la aceasta. Această problemă este elaborat
Shannon în „Lucrări selectate pe teoria informației.“ Dacă mesajul
un eveniment care apare frecvent, din care probabilitatea este aproape de unitate, care este un mesaj pentru destinatar puține informații. La fel cum puține informații raportate Soby-tiyah, din care probabilitatea este aproape de zero.

Evenimentele pot fi văzute ca un rezultat posibil al unei anumite experiențe, precum și toate rezultatele acestei experiențe, formează un grup complet de evenimente. Shannon a introdus conceptul de incertitudine a situației apărute în cursul experimentului, numindu-l entropică.

Entropiyapolnoy grup de evenimente este o măsură cantitativă a incertitudinii sale și, în consecință, TION, conținutul informațional cantitativ exprimat ca funcție medie probabilitatea de set-citatea fiecăruia dintre rezultatele posibile ale unui experiment. Cantitatea de informații obținute în urma experimentului, aceeași incertitudine este îndepărtată în timpul acestei experiențe.

O abordare probabilistică este cel mai bine explicată printr-un exemplu care implica zarului corect aruncator clorhidric având N fațete (cea mai comună este cazul hex os: N = 6). Rezultatul acestui experiment poate fi pierderea de fata cu una dintre următoarele caractere: 1, 2. N.

Luați în considerare cantitatea numerică care măsoară incertitudinea - entropie (notată cu H). Valorile H și N sunt legați o relație funcțională:

iar funcția f este în creștere, iar nenegative definit (în exemplul considerat) pentru N = 1, 2. 6.

Procedura de aruncare de zaruri:

- obtinerea gata pentru a arunca un os. Rezultatul Experiența nu este cunoscut, și anume Există o oarecare incertitudine, vom nota H 1;

- os aruncat. Informații cu privire la rezultatul acestui experiment este obținut, această cantitate de date este notată cu I;

- denotă incertitudinea experimentului după punerea sa în aplicare prin H2.

Pentru cantitatea de informații obținute în timpul experienței exercițiu, să ia incertitudinea diferența „înainte“ și „după“ experiment:

Evident că, în cazul în care se obține rezultatul specific, care a îndepărtat incertitudinea (H 2 0). Numărul de informații primite coincide cu entropia originală. Cu alte cuvinte, incertitudinea conținută în experiența, în concordanță cu informațiile cu privire la rezultatul acestei experiențe. Semnificație H 2 ar putea fi de zero, de exemplu, în cazul în care în timpul experimentului a avut următoarea fațeta cu o valoare mai mare de trei.

Următorul lucru este de a determina tipul funcției f. Dacă varia numărul de fețe N și numărul de aruncări zaruri (această valoare este notat cu M). Numărul total al rezultatelor (M vectori de lungime 1 format din caractere, 2. N) este egal cu N în gradul de M:

Astfel, în cazul a două aruncări de zaruri cu șase laturi, avem: X = 6 2 = 36. De fapt, fiecare X este rezultatul unei anumite perechi (X1, X2) unde X1 și X2 - respectiv, prima și a doua rezultate ale mulaje (totale astfel de perechi - X).

Situația cu exprimate de M ori osul poate fi privit ca un sistem complex format din subsisteme independente reciproc - „aruncări unice oasele.“ Entropia unui astfel de sistem este de M ori mai mare decât entropia unui sistem (așa-numitul „principiul aditivitatea entropiei“):

în cazul în care * - semn de multiplicare.

Din formulele de măsură derivată Hartley:

Important cu introducerea unei cantități este întrebarea de ce să ia pentru unitatea de măsură. H este egal cu unu atunci când N = 2. Cu alte cuvinte, ca unități de informații numărul de informații primite asociate cu efectuarea unui experiment care constă din primirea unuia dintre cele două rezultate la fel de probabile (un exemplu al unui astfel de experiment poate servi ca aruncarea monedei în care sunt posibile două rezultate: „Eagle "" cozi „).

În cazul în care probabilitățile de rezultate diferite nu experiență în mod egal (dar au o probabilitate Pi), o măsură a entropiei se calculează cu ajutorul formulei Shannon:

Ca un exemplu, să definească cantitatea de informații asociate cu apariția fiecărui personaj în mesaje scrise în limba rusă. Presupunem că alfabetul românesc este format din 33 de litere și semnul „spațiu“ pentru a separa cuvinte. Conform formulei obținem: n> 5 biți.