Caracteristici capac închis și procesele din ele, pagina 2
.
Funcția de răspuns impuls este cuprinzător PAC caracteristică dinamică, în sensul că, știind că, este întotdeauna posibil să se determine răspunsul SAR la orice impact.
Definirea funcției de transfer, rezultă că, în (2) va fi la sau imagini laplaciană:
pentru (vezi. Tabelul 2.1.)
Substituind aceste expresii în (2), constatăm că
.
Dacă această expresie aplică inversă transformatei Laplace, apoi pe partea stângă, în conformitate cu (3) avem funcția de răspuns la impuls, iar pe partea dreapta - un derivat al tranziției de o funcție de timp (vezi Tabelul 2.2.):
ecuația ATS în domeniul timp poate fi obținut prin aplicarea (2) Inverse Laplace transforma și folosi teorema convoluție (Tabelul 2.2):
.
Să ne amintim că funcțiile sunt originale, caracteristici care, cu un argument negativ la zero.
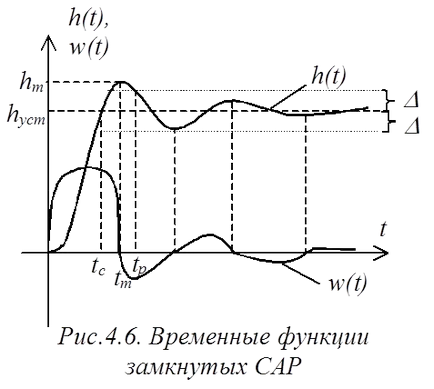
hSet - valoare la starea de echilibru a funcției de tranziție (coordonate controlate);
hm - valoarea maximă;
D - valoarea care definește vecinătatea hSet. în care procesul poate fi considerat ca fiind stabilit (de obicei, în sistemele tehnice);
tc - prima coordonare a funcției de tranziție pentru a seta valoarea;
tm - timp pentru a ajunge la funcția de tranziție valori hm;
tp - timp de control, după care procesul de tranziție va intra într-o zonă și mai mult din ea va veni.
cifre provizorii tc. tm. caracterizează tp performanța SAR.
oscilație PAC caracterizată prin depășirea. care este de obicei măsurată în procente:
.
Conceptul de proces liber și constantă.
ATS de reacție (Figura 4.5) printr-o expunere arbitrară poate fi determinată din expresia:
unde t - monitorizarea în timp a reacției AAR.
După cum se cunoaște din SOC rata, o tranzitorie într-un sistem care funcționează în mod normal, toate valorile (coordonatele SAR) constau din componente de echilibru (intern) și libere.
Astfel, pentru ATS dat dacă vom lăsa expresia (1) va fi forțat să descrie procesul. care apare după toate componentele de dezintegrare libere
.
.
,
pentru că. Al doilea factor este nimeni altul decât ATS la PD, adică, .
Din această expresie este clar că procesul de expunere intermitentă forțată este independentă de timp și proporțional cu zona delimitată de răspunsul la impuls al ATS:
.
Astfel, procesul indus de DC (hopping) expunerea este produsul dintre amploarea acestui efect asupra PD la.
Același rezultat poate fi obținut, dacă luăm în considerare faptul că în acest exemplu (tabelul 2.1) și utilizarea teorema finală (tabelul 2.2), prin care
.
De exemplu, Figura 4.8 pentru procesul PAC ar fi obligat să:
.
Exemplul 2. Pentru a determina când o acțiune armonică proces forțat
.
.
.
Al doilea factor este PF PAC la.
.
Dependența se numește frecvența funcției de transfer al ATS.
Astfel, procesul de acțiune armonice forțate este de asemenea frecvență armonică și este egală cu produsul funcției la intrare de funcționare.
Caracteristicile de frecvență și semnificația lor fizică
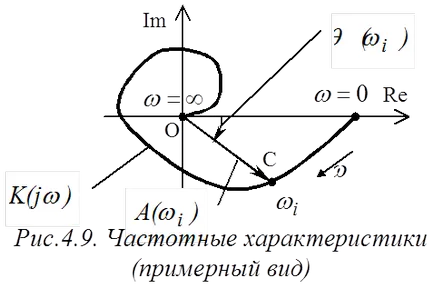
Funcția SAR Frecvența este reprezentată grafic pe planul complex atunci când schimbă frecvențele semnalelor armonice de la zero (sau de la) înainte (Figura 4.9). Un astfel de program schimbă funcția de frecvență poziția locus în timp ce schimbarea frecvenței se numește răspuns la frecvență.
,
unde - amplitudinea de frecvență caracteristică (AFC) AAR egală cu lungimea frecvenței locusului caracteristică (figura 4.9);
- faza de răspuns (PFC) AAR poziție unghiulară egală a locusului răspunsului în frecvență (Figura 4.9).
Astfel, răspunsul în frecvență este factorul de transfer între amplitudinea unei armonici a semnalului de intrare și amplitudinea semnalului de ieșire. Cu alte cuvinte, valoarea frecvenței de răspuns la o anumită frecvență armonică a semnalului de intrare este raportul dintre amplitudinea de ieșire la amplitudinea semnalului de intrare.
FRF caracterizează trecerea fazei semnalului de undă de ieșire în raport cu intrare. În cazul în care semnalul de ieșire se situează în faza a semnalului de intrare, în caz contrar - înainte.
Astfel, în cazul în care ATS este operabil, atunci când acțiunea de intrare după semnalul de ieșire tranzitorie va avea forma:
.
Exemplu. Construiți o frecvență caracteristică a PAC cu PF
,
în cazul în care - unii coeficienți.
Decizie. Scrieți expresiile pentru caracteristicile de frecvență:
;
;
.
Bazându-se pe planul complex la schimbarea de la 0 la (Fig.4.10) Keypoint:
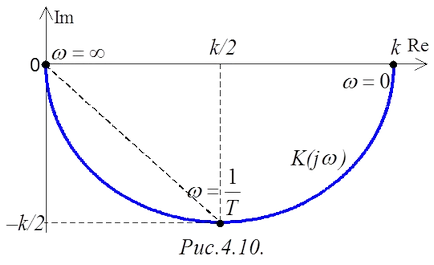
Este evident că frecvența scade odată cu creșterea, dar crește. De fapt, răspunsul în frecvență va fi sub forma unui semicerc (Fig.4.10). Grafică aceeași frecvență imagine și faza de răspuns va fi foarte incomod pentru percepția, însă utilizarea așa-numitul răspuns de frecvență logaritmic.
Caracteristica logaritmică amplitudine-frecvență (LACHH) se numește relație
,
care este construit în axele w lg. L (figura 4.11).
faza de răspuns logaritmică (LFCHH) este dependența care este construit în lg w axe. q (figura 4.11).
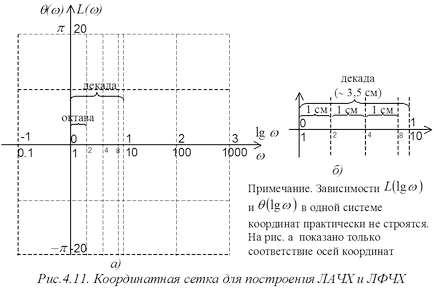
Segmentul pe abscisă, corespunzător unei creșteri a frecvenței de 2 ori, numită octavă; creștere corespunzătoare a frecvenței de 10 ori - deceniu.
La construirea LACHH și LFCHH manual pe hârtie într-o celulă, puteți utiliza octavă relații aproximative și deceniu dat pe ris.4.11b.
De exemplu, pentru exemplul de mai sus, atunci când k = 2. T = 0,1 LACHH LFCHH și au forma prezentată în ris.4.12.
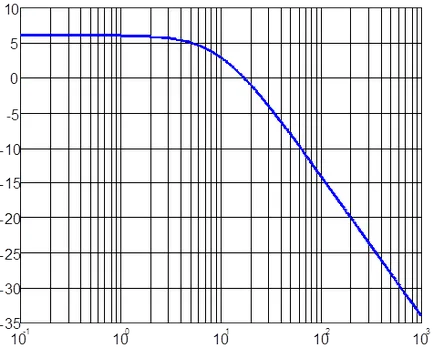
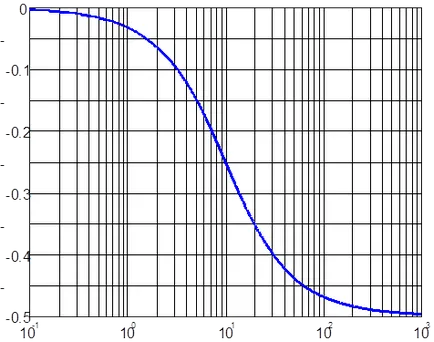
Ris.4.12. LACHH (a) și LFCHH (b), de exemplu, de ATS.