Calcularea suprafeței de forme complexe, folosind metoda de simulare

Calcularea suprafeței de forme complexe, folosind metoda de simulare

Sarcina: Dezvoltarea unui program care permite metoda de simulare pentru a calcula o suprafață complexă a figurii delimitată de partea superioară a curbei U = Y1 (x). sub V = Y2 (x).

1. Următoarea metodă poate fi utilizată pentru a rezolva această problemă.

Limitat la o anumită cifră a unui dreptunghi ale cărui laturi sunt:

prin punctele de valorile minime și maxime ale funcțiilor și axele abscisă sunt paralele;

prin punctele de frontieră din stânga și din dreapta ale argumentului definiție și paralelă cu axele ordonatei.

Cu ajutorul senzorului de numere aleatoare a jucat punct aleatoriu coordonatele acestui dreptunghi. Verificați punctul de cădere într-o anumită formă. Cunoscând aria unui dreptunghi și atitudinea a primit puncte pentru numărul total de jucat, este posibil să se estimeze zona de interes pentru noi figuri.

2. Caracteristici tehnice ale obiectului de cercetare:

2.1. Intervalul de valori ale parametrilor problemă.

O multitudine de curbe limită ale treia Polinoamele de ordine, deoarece polinoamele de ordin superior crește foarte mult timp de calcul. Mai mult decât atât, pentru claritate, soluția este destul de mult despre „3“.

Coeficienții intervalului limită polinomială [-100.100].

FIELD interval de determinare limită [-100.100].

Aceste limite sunt proiectate pentru a rezolva o problemă vizuală, și nu pentru a le schimba din punct de vedere tehnic, nu este dificil.

3. Soluția problemei.

Această problemă a fost rezolvată în Turbo C. mediu pentru a rezolva problema generală necesară pentru a împărți în mai multe sarcini mici (proceduri).

Și anume sarcini separat (sub formă de proceduri) au fost rezolvate

-mesaj de eroare atunci când introduceți;

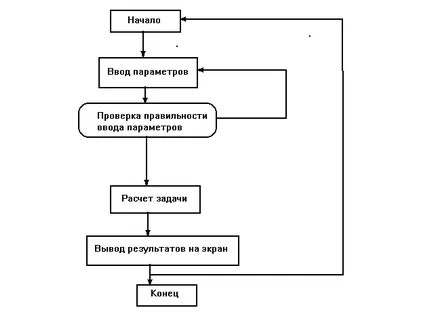
4. O descriere a procedurilor utilizate în program.

4.1 window.c fișiere.

4.1.1 Procedura pentru introducerea parametrilor.

void get_poly (float * b3, float * b2, float * b1, float * B0 // - coeficienții polinomului Y1

fliat * c3, float * c2, float * c1, float * c0, // - coeficienții polinomului Y2

float * x1, x2 float *, // domeniul de [x1, x2]

int * N) // numărul de apeluri către generator de numere aleatoare //

4.1.2 Procedura de elaborare a cadrului ferestrei.

void frontieră (int sx, int sy, int en, int ey) // atrage cadrul cu coordonatele colțul din stânga sus // (sx, sy) și coordonatele colțul din dreapta jos // (ex, ey)

4.1.3 Procedura de comunicare a erorilor pe măsură ce tastați.

Procedura emite un semnal sonor și afișează un mesaj de eroare în cazul în care intrarea.

4.2.1 Procedura de calculare a valorilor maxime și minime ale funcțiilor la un interval predeterminat.

void f_max (float b3, float b2, float b1, float B0 // - coeficienții polinomului Y1

fliat c3, float c2, float c1, float c0, // - coeficienții Y2 polinomului

float x1, x2 float, // domeniu [x1, x2]

float * amin, float * amax) // valorile maxime ale funcțiilor minime și //

4.2.2 Procedura de calculare a valorilor polinomului la un anumit punct.

float distracție (b3 float, float b2, b1 float, b0 float, // - coeficienți polinomiali

Returnează valoarea polinomului la x.

4.2.3 Procedura de calcul rădăcina cubică a ecuației.

f_root int (float b3, float b2, float b1, float B0 // - coeficienții polinomiali Y1

fliat c3, float c2, float c1, float c0, // - coeficienții Y2 polinomului

float x1, x2 float, // domeniu [x1, x2]

float e, // rădăcini precizie de calcul

float * k1, float * k2, float * k3) // Valori // funcții rădăcină

Returnează numărul de rădăcini reale în intervalul.

4.3. fișier F_INTEGER.C

4.3.1 Procedura de calcul a zonei de forme complexe prin metode numerice.

float f_num (b3 float, float b2, b1 float, b0 float, // - coeficienții polinomiali Y1

fliat c3, float c2, float c1, float c0, // - coeficienții Y2 polinomului

float x1, x2 float) // domeniu [x1, x2]

Calculează aria complexă a figurii.

4.3.2 Procedura pentru calcularea suprafeței unei forme complexe, folosind metoda de simulare c modelrovaniya

float f_ (b3 float, float b2, b1 float, b0 float, // - coeficienții polinomiali Y1

fliat c3, float c2, float c1, float c0, // - coeficienții Y2 polinomului

float x1, x2 float, // domeniu [x1, x2]

float fmin, float fmax, // valorile minime și maxime ale funcțiilor // în acest interval

int n) // numărul de accese la un generator de numere aleatoare //

Calculează aria complexă a figurii folosind metoda de simulare.

4.4.1 Inițializarea modul grafic de rutină.

4.4.2 Procedura de cursă buclă continuă.

void f_draft (float b0, float b1, b2 float, float b3, // - coeficienți polinomiali

float x1, x2 float) // domeniu [x1, x2]

4.4.3 Procedură vyrisovki axelor.

osi void (float x1, x2, float // funcții de domeniu

float b) // Coeficientul mashtabnykh calculat prin formula

// b = j - Fmin * (i-j) / (Fmax - Fmin)

// unde i, j - a seta pozitia grafica de pe ecran

// Fmin, Fmax - valorile minime și maxime ale funcțiilor // în acest interval

4.5 DRAFT_F fișiere.

4.5.1 grafice Procedura vyrisovki.

void draft_f (float b3, float b2, float b1, float B0 // - coeficienții polinomului Y1

fliat c3, float c2, float c1, float c0, // - coeficienții Y2 polinomului

float x1, x2 float, // domeniu [x1, x2]

float fmin, float fmax, // valorile minime și maxime ale funcțiilor // în acest interval

int k, int i, int l, int j) // coordonatele care definesc poziția grafica pe ecran //

4.6 DRAFT_N fișiere.

4.6.1 grafice Procedura vyrisovki polschadey valori Calculați metoda chislvym și simularea în funcție de numărul de accese la generatorul de numere aleatorii.

void draft_e (float b3, float b2, float b1, float B0 // - coeficienții polinomului Y1

fliat c3, float c2, float c1, float c0, // - coeficienții Y2 polinomului

float x1, x2 float, // domeniu [x1, x2]

float fmin, float fmax, // valorile minime și maxime ale funcțiilor // în acest interval

float Sn, // suprafață calculată numeric de

int k, int i, int l, int j) // coordonatele care definesc poziția grafica pe ecran //

Toate fișierele sunt unite în programul principal SQ.C, care este principalul și coordonează procedurile de lucru.

5 Utilizarea programului.

Pentru a utiliza acest program necesită mediu de operare MS DOS,

fișier egavega.bgi, și, de fapt, ea a întocmit programul sq.exe.

6 Codul sursă este dat în apendicele №1.

7 exemplu scândură este prezentată în Anexa №2.

8 Referințe.

1. limbajul de programare C pentru PC. SO Bochkov, DM Subbotin.

2. C ++. Descrierea limbajului de programare. Bjarne Straustrap.

3. TURBO C. Ghidul utilizatorului. Borland International, Inc. 1988.

4. TURBO C. Ghid de referință. Borland International, Inc. 1988.

9.1 Compararea rezultatelor cu terbovaniem de locuri de muncă.

9.2 Recomandări pentru îmbunătățirea programului.

oportunități de a îmbunătăți programul în dezvoltarea de algoritmi de intrare a diferitelor clase de funcții.

Anexa 1. Textul programului.

Programele principale SQ va