Calcularea momentului de inerție al pendulului

Obiectiv -Determinarea pendulului momentul de inerție, folosind ecuația undelor și studiul momentului de inerție al distanței de la punctul selectat în mod condiționat A.

Instalația este un pendul fizic, adică solid, pendulează sub influența gravitației pe axa orizontală nu trece prin centrul său de masă.

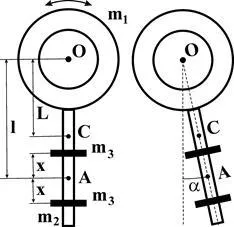
pendulului fizic în această lucrare constă într-o masă m1 tambur cu axa de rotație O. m2 masă tijă și două sarcini cu mase identice m3. care poate fi fixat în poziție pe tija (fig.5.1).

Calcularea momentului de inerție al pendulului

În timp ce gravitația R. aplicată în centrul de masă C este direcționată de-a lungul axei tijei (fig.5.1 „a“), sistemul este în echilibru. În cazul în care respinge PIN-ul la un unghi mic (figura 1 „b“) cu centrul de masă situată la o înălțime și corp mic câștigurile de alimentare cu energie potențială. Un pendul despre direcția axei OA este ales „noi“, este în același timp gravitatea actului, a cărei proiecție pe această axă este

în cazul în care; L - distanța dintre axa de rotație O și centrul de masă C.

Cuplul generat de puterea lui M. R., la mici unghiuri egale

.

Aceasta determină accelerarea mișcării de rotație a pendulului. Comunicarea dintre forțele de accelerație și un cuplu dat ecuația fundamentală a dinamicii mișcării de rotație

unde J - momentul de inerție al pendulului în raport cu axa O.

Apoi, din ecuația (5.2), obținem