ASTRONET - AO tutorial 1 turbulență
- - intensitatea luminii în planul focal ca funcție unghiulară de coordonate;
- - lungime de undă a luminii;
- - telescop deschidere diametru;
- - așa-numita funcție Bessel.
Primul inel întunecat este situat la o distanță unghiulară de centru. Adesea, această distanță este considerată a fi o măsură a rezoluției unui telescop ideal.
Imagine obiect astronomic poate fi privit ca o multitudine de pixeli de imagine, fiecare dintre acestea fiind descrise de funcția Airy. Acest lucru poate fi scris ca convoluție.
Noi numim această imagine ecuație. Comparativ cu imaginea de obiect o mai lin, rezoluția scade. Cu toate acestea, pentru un anumit diametru al telescopului această deteriorare - cel mai mic posibil. În acest caz, se spune că rezoluția imaginii este limitată de difracție. EXEMPLU imagini astronomice (centrul galactic) cu diferite rezoluții de mai jos.
Î: Cum rezoluția lor de difracție limitele depinde de lungimea de undă?
Întrebare: Calculati rezoluția limitată de difracție a ochiului uman.
Ce se întâmplă în cazul în care telescopul nu este ideal? Imaginea unei surse punct nu este la fel de bun ca funcția Airy, rezoluția se va deteriora și mai mult. Dar imaginea ecuația va rămâne în vigoare! Astfel, funcția point spread (PSF) - aceasta este tot ceea ce este necesar pentru a caracteriza imaginea. Lățimea PSF - este o măsură a rezoluției.
Nota 1. Implicit, am presupus că, în ecuațiile de mai sus descrie imaginea stelei de intensitate unitate, și anume, Este egală cu integrala de peste 1. Astfel, ecuația își păstrează fluxul plin de imagine dintr-un obiect astronomic, doar diferit distribuie la pixeli.
Nota 2. Am presupus că PSF are aceeași formă pe toată suprafața câmpului vizual. Această condiție se numește isoplanatism. Acest lucru nu este întotdeauna adevărat pentru imagini astronomice, mai ales atunci când se utilizează AO, deoarece PSF se schimbă încet peste câmp. În acest caz, ecuația de formare a imaginii pot fi aplicate la părți ale câmpului vizual.
Forma PSF poate fi neregulată; în acest caz, pentru a cuantifica rezoluția?
1. lățimea la jumătate maximă (FWHM) PSF.
2. Numărul de raport Strehl, adică, intensitatea centrală PSF în comparație cu intensitatea centrală a funcției Airy. Cu cât raportul Strehl, cu atât mai bine rezoluția. imagine limitată Difracția - cel mai bun, ca întotdeauna.
3. Energia în cerc. Prin definiție, integralei PSF este egal cu 1. Integrala PSF din raza cercului se numește energia în cerc. Această caracteristică este importantă pentru observarea obiectelor de leșin atunci când aveți nevoie cel mai bun posibil să se concentreze fotoni.
Exemplul PSF cu corectarea turbulență este prezentată mai jos.
Întrebare: Să presupunem că PSF a devenit deja de două ori, cum de a schimba raportul Strehl?
Întrebare: Care va fi raportul Strehl, ideală dacă jumătate a cristalinului telescop pentru a da o întârziere de fază a?
Un alt mod de a descrie imaginea ecuației - este utilizarea transformatei Fourier (FT, va fi notat cu tilda). Convoluție devine o lucrare, și
Modelul Kolmogorov distorsiunilor de turbulență prescrie forma specifică a funcției structurii de fază, și anume,
În această formulă, un singur parametru, care se numește raza coerenta atmosferică sau parametru Fried. Având în vedere că lungimea traseului este acromatic, am înțeles. Definirea întotdeauna se referă la lungimea de undă corespunzătoare!
Acest model, deși poate părea primitiv, este fundamentul întregii teorii a imagistica prin turbulență, inclusiv sisteme optice adaptive. Desigur, modelul nu funcționează bine pe mare (mai mult de câțiva metri) și mici (mai puțin de 1 cm) la distanță, dar se pare că acest lucru nu este foarte important.
Vorpos: Care este diferența pătratică medie a lungimii de fază atmosferică a bazei în radiani și lungimi de undă?
Întrebare: În cazul în care se vedea la o lungime de undă de 0,5 microni, care este încă la o lungime de undă de 2,2 microni?
Acum am pus acest model în expunerile lungi atmosferice OTf și să-l sub formă de:
Aplicând transformata Fourier a acestei ecuații, obținem PSF atmosferic pentru expunerile lungi. Calculele numerice se obține relația dintre FWHM PSF atmosferice (numite sau o calitate a imaginii), și:
La o lungime de undă de 0,5 microni, calitatea imaginii 1 secundă corespunde = 10,1 cm.
Raportul Strehl PSF atmosferic este exact la fel ca și pentru un telescop perfectă (aceasta este cauza factorului ciudat 6,88) Astfel, pentru un telescop mare, raportul Strehl este simplu.
Întrebare: Care este raportul Strehl pentru o imagine cu o expunere lungă la 4 m telescop la calitatea imaginii de 1 secundă la lungimi de undă de 0,5 și 2,2 microni?
raza Fried, uneori identificat cu perturbațiile atmosferice la scară caracteristică. Acest lucru nu este destul de adevărat: vedem că legea Kolmogorov nu are nici o scară caracteristică. Cu toate acestea, doar o perturbație la dimensiunea comenzii sunt importante pentru imagini cu expuneri lungi. Pe o scară mai mică distorsiune este mult mai mică decât pe scară largă devine atât de mare încât OTF atmosferic este zero.
Amplitudinea locală a fluctuațiilor turbulente ale indicelui de refracție în aer este descrisă de structura constanta a indicelui de refracție, care se măsoară în unități de ciudat, m. Dependența de profilul de înălțime se numește turbulențe. Calitatea imaginii depinde de efectul combinat al tuturor straturilor ale atmosferei:
în cazul în care - înălțimea, - unghiul zenital și integrarea este realizată de telescopul la înălțimea maximă a turbulenței (aproximativ 20 km).
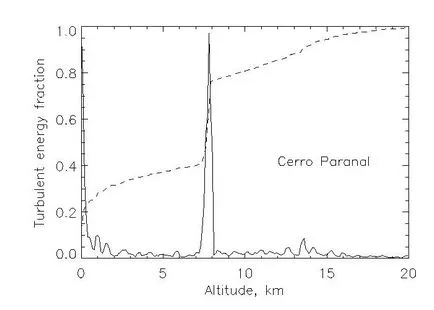
Această figură prezintă un exemplu de profil de turbulență în unități relative în Cerro Paranal (linie solidă). Raportul de energie turbulentă într-o anumită înălțime reprezentat de linia punctată. Deși în acest exemplu, o parte semnificativă a turbulenței este concentrată în două straturi, încă aproximativ 1/3 din energia totală este distribuită uniform pe toate înălțimile.
Întrebare: Folosind această relație, pentru a primi ca o calitate a imaginii depinde de unghiul de înclinare.
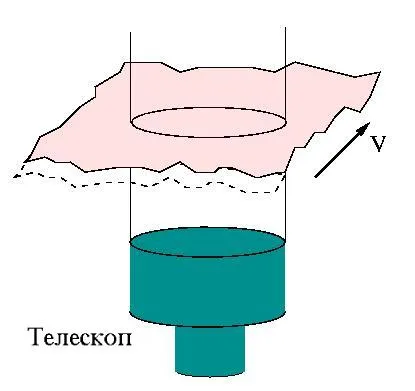
în cazul în care - viteza vântului, înălțimea medie. Acest parametru definește cât de repede ar trebui să fie un sistem de sisteme optice adaptive.
Q. Luând valoare tipică = 20 m / s, care este timpul atmosferic constant la lungimi de undă de 0,5 și 2,2 microni, cu o imagine de la 1 secundă?
Imagini de obiecte cerești luate cu expunere sau mai scurte sunt numite imagini de scurtă expunere. Ele corespund fixe (înghețate) de aberații atmosferice. Pentru expuneri mai lungi sunt aberații, medii și expunerile mult mai mult timp puteți obține un PSF-expunere lungă.
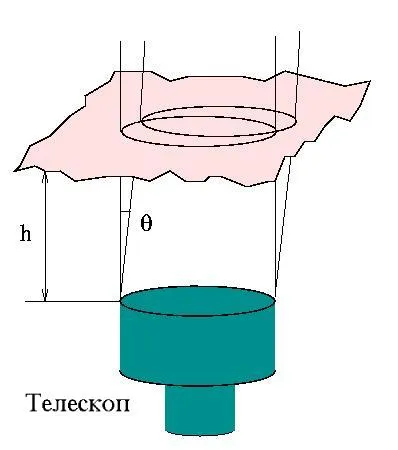
Definiția standard a unghiului isoplanatic atmosferic - l
în cazul în care - este o caracteristică altitudine medie de turbulență. Ia medie ponderată cu profilul, ca urmare, pentru condițiile tipice ale unui suficient de mare înălțime km.
Întrebare: Care este unghiul isoplanatic pentru lungimile de undă de 0,5 și 2,2 microni, cu o imagine de la 1 secundă?
Acest fenomen este o problemă foarte mare pentru sisteme optice adaptive, deoarece limitează distanța dintre steaua de referință și obiectul în studiu. Se pare că pentru majoritatea obiectelor nu este adecvat (cele luminoase) stele de referință, astfel încât aveți nevoie de ghidare cu laser artificiale stele. Ca o metodă alternativă, pentru a crește câmpul corectat, puteți încerca să aplicați corecția tri-dimensională de turbulență (sisteme optice adaptive multi-conjugat. MCaO).
În optica, aberațiile sunt reprezentate adesea ca o sumă de polinoame speciale, numite polinoame Zernike. aberații atmosferice aleatorii pot fi prezentate în aceeași formă; cu toate acestea, coeficienții acestor aberații (defocalizarea, astigmatismul, etc.) sunt funcții aleatoare care variază în funcție de timp.
polinoamele Zernike sunt determinate în coordonate polare pe circumferința unității rază. Ele sunt caracterizate prin ordin ordine radială și azimutal (pentru aceasta, ia valori între 0). De multe ori, în loc de cei doi indici și numerotarea consecutivă cu un singur indice. Pentru un ordin radial dat exista polinoame Zernike.
Primele moduri Zernike sunt denumite la fel ca aberațiile cunoscute, și au un înțeles simplu (a se vedea tabelul din primele 15 moduri Zernike).
Avantajele utilizării modurilor Zernike decurg din faptul că acestea sunt ortonormal. adică produsul scalar este egal cu 1 dacă și zero, în alte cazuri. Produsul scalar este definit ca fiind integrala deasupra deschiderii telescopului:
Numărul limitat de multe ori moduri de Zernike oferă deja o reprezentare destul de bun de aberații atmosferice. Dacă aceste moduri sunt corectate optice adaptive, creează o imagine cu o calitate care este practic imposibil de distins de difracție determinată.
piston de moda corespunde unei faze constantă, care nu afectează imaginea. În mod normal, acest mod este ignorat.
Întrebarea 4-m telescop defocalizat cu 1 mm. Se calculează aberației care apar pentru 0,5 lungimi de undă și 2,2 microni.
Întrebare: Să presupunem că aberația atmosferică conține numai pante aleatoare cu amplitudini egale. Functia de structura de fază corespunzătoare.
Modurile ortonormalitate Zernike oferă o modalitate simplă de a calcula o fază de dispersie, integrat pe elev. Pentru un singur mod este. Dispersia tuturor modurilor este suma pătratelor coeficienților, pornind de la al doilea (piston exclus).
In modelul de turbulență Kolmogorov, putem obține proprietățile statistice ale coeficienților care corespund aberațiile faze atmosferice. transformări matematice conduc la o formulă simplă:
După cum puteți vedea, matricea Noll este aproape diagonală (dar acest lucru nu este cazul pentru comenzi mai mari). De ce nu există nici un factor? Pentru Kolmogorov turbulență este infinit! Cu toate acestea, primul modul (piston) este irelevant pentru imaginea.
Întrebare: Pentru 4 și calitatea imaginii a doua telescop 1, calcula RMS amplitudinea încline în radiani (la lungimea de undă de 0,5 microni). Mutați-l la rms amplitudinea mișcării imaginii stele. Depinde dacă amplitudinea lungimii de undă?
Ce se întâmplă dacă am corecta prima moda folosind sisteme optice adaptive? Coeficienții corespunzători devin zero, iar scăderea totală de dispersie în fază. Denotă medie peste pupile fazei de dispersie așa cum scrie
în cazul în care sunt corectate primele moduri Zernike.
Full necorectată variație de fază atmosferică (toate modurile cu excepția pistonului) se potrivește. Cu alte cuvinte, un telescop cu un diametru deschidere fază atmosferică variație este de aproximativ 1 radiani pătrați. Dacă panta este corectată, atunci. Acest lucru înseamnă că pante de 87% din faza de dispersie totală. Corectarea mod radial aproximativ 2 pentru a obține ordinea radială a 3 frunze dispersie necorectat. După cum puteți vedea, reducerea în continuare a fazei de corecție a variației necesită un număr tot mai mare de moduri Zernike.
Pentru un număr mare de moduri fixe (10 $ „width =“ 61 „height =“ 34 „> care apare în sistemele reale), o formulă asimptotic foarte util pentru Noll:
Întrebare: Folosind valorile și datele de mai sus, se calculează.
Cât de multe moduri trebuie corectate? Optica știu că, atunci când faza reziduală este mai mică de 1 radian, calitatea imaginii se apropie de limita de difracție. Acum avem tot ce ai nevoie pentru a determina numărul de moduri în funcție de diametrul telescopului, calitatea imaginii și lungimea de undă! Este suficient pentru a înregistra și înapoi toate formulele (încercați să-l facă!). rezultatul
Î: Câte Zernike moduri trebuie corectate la 4 m telescop pentru imagistica la lungimi de undă de 0,5 și 2,2 microni, cu o imagine de la 1 secundă?
Este necesar să se corecteze turbulențele folosind modurile Zernike? Desigur, nici aberații de fază pot fi măsurate și corectate cu ajutorul oricărui alt set de funcții de bază sau moduri, în general, fără a afecta direct Wavefront. Se pare că modurile de Zernike - aceasta este al doilea set de evenimente de calitate (cel mai bun set de moduri numit Karhunen-Loev). Alegerea depinde de numărul de parametri monitorizați (evenimente) necesare pentru a atinge gradul dorit de corectare; pentru modurile Zernike este mai mică decât pentru un control local, a frontului de undă.
Concluzii. În acest capitol, fundamentele unei imagini într-un telescop ideală și prezenței aberațiilor (PSF, OTF, limita de difracție, raportul Strehl). Apoi, parametrii de bază ai atmosferei referitoare la o optică adaptativă (funcție de fază structura, calitatea imaginii, constanta de timp și unghiul de isoplanatic). Am studiat descompunerea aberațiilor de fază aleatoare pe modurile Zernike. Acum putem determina numărul de evenimente care trebuie corectate.