asimptotă hiperbola

Direct. la care se apropie în mod arbitrar aproape de curba de la punctul (ramuri curba) pentru mișcarea sa de-a lungul curbei spre infinit, hiperbolice numit asimptota.

Referindu-ne la diagonalele MNKL dreptunghiului formează ecuația liniei OK (Figura 22):

utilizarea directă ecuație „beam“ pentru prepararea ecuației. atunci.

Scriem ecuația liniei în forma generală:

Găsim distanța de la punctul de la linia de hiperbolă OK, folosind formula de calcul distanța de la un punct la o linie.

Inmultiti numărătorul și numitorul fracției pe. obținem

(. X0 y0) Deoarece M0 - punctul de hiperbolă, coordonatele sale satisfac ecuația hiperbola (1), apoi (A se vedea „Derivarea hiperbolă.“), Atunci:

Din această formulă rezultă că, atunci când se deplasează de-a lungul unei hiperbolă, astfel încât x0 sale abscisă crește la infinit (și deci numitorul fracției crește), apoi distanța până la linia scade la infinit, adică - asimptota hiperbolă.

Aceeași împrejurare se va produce la punctul M curge de-a lungul unei hiperbolă în al treilea trimestru (prin simetrie cu privire la originea).

În cele din urmă, vom obține un al doilea rând, datorită simetriei hiperbola în raport cu axa OY. dispuse simetric drepte. la care, de asemenea, se va apropia la infinit punctul M în timp ce se deplasează de-a lungul unui hiperbolă, și la o distanță de infinit (în al doilea și al patrulea quadrants).

Aceste două linii sunt numite asimptote ale hiperbola (Fig 25).

Ecuațiile asimptote ale hiperbola:

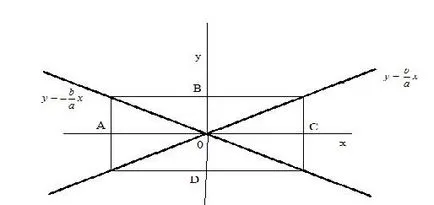
asymptotes hiperbolă sunt aranjate de-a lungul diagonalelor „miez“ hiperbolă dreptunghi, dintre care o parte este paralelă cu axa OX și egală cu 2a. cealaltă - paralelă cu axa OY și este egală cu 2b. iar centrul este la origine.

În construcția de hiperbole în ecuația sa trebuie să construiască primul său asimptota.

Construiește hiperbola (Fig.26)

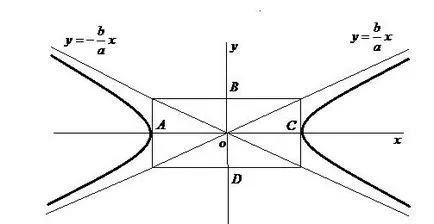
În mod similar, putem efectua un studiu al ecuației (4.2)

și de a construi o hiperbolă (fig.27)