aplicație educațională a metodelor numerice de aproximare a unei funcții

Metoda spline cubice

Originea termenului „spline“ este conectat cu un desen liniar flexibil, care a fost utilizat pentru desenarea curbelor netede care trec prin punctele date.

Spline de interpolare - un mod rapid, eficient și durabil a funcțiilor de interpolare. Alături de interpolare rațională, spline de interpolare este o interpolare polinomială de alternative [28].

Interpolarea bază spline bazat pe următorul principiu. interval de interpolare este împărțit în segmente mici, fiecare dintre care este definit printr-o funcție polinomială de gradul III. Coeficienții polinomului sunt selectate astfel încât să îndeplinească anumite condiții (care depinde de metoda de interpolare). Comun pentru toate tipurile de cerințe spline de ordinul al treilea - funcții continue și, desigur, trecerea prin punctele atribuite. Cerințe suplimentare pot fi o funcție liniară între noduri, continuitatea derivatelor superioare, etc.

Principalele avantaje ale interpolarea spline este stabilitatea acesteia și complexitate redusă. Liniar sistem ecuații care trebuie rezolvată pentru a construi spline, foarte bine conditionat, care permite obținerea coeficienților polinoamelor cu mare precizie. Ca rezultat, chiar și cu privire la schema de calcul foarte mare N nu-și pierde stabilitatea. spline Masa Coeficientul de construcții necesită operații O (N), și calcularea valorii spline la un anumit punct - numai

In general cubic spline polinomiale selectat

definit în intervalul.

Întreaga curbă este un set de polinoame cubi (figura 1.4) cu coeficienți aleși corespunzător - parametrul spline [20, 38].

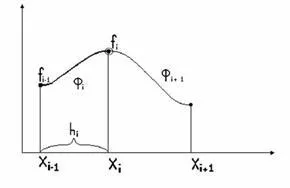
Figura 1.4: Schema de metode spline

Coeficienții pentru fiecare interval sunt determinate de condițiile de transmisie în nodurile:

În plus, la frontieră, atunci când sunt stabilite condițiile și

Noi căutăm un polinom cub în formă

Din condiția avem

și necesită o continuitate a acestora la.

Numărul total de coeficienți necunoscuți este, evident, egal. numărul de ecuații (1.13) și (1.14) este egal. Lipsesc două ecuații pe care le primim de la (1.12) pentru u.

Expresia (1.14). Substituind această expresie în (1.13) și excluderea. obținem:

Acum substituind expresiile pentru prima + în formula (1.14), după transformări simple, pentru determinarea ecuație diferență de ordinul:

Cu condițiile la limită:

Și condiția este echivalentă cu ecuația. Ecuația diferența (1.15) cu condițiile (1.16) pot fi rezolvate prin metoda matura, reprezentată ca un sistem de ecuații algebrice liniare ale formei. unde vectorul corespunde vectorului. vector F este element înțelept din partea dreaptă a ecuației (1.15), iar matricea A are următoarea formă:

metodă, bazată pe presupunerea că necunoscutele necunoscute sunt legate de relația de recurență matura:

Folosind această relație, putem exprima și prin și substitui ecuația i-e:

în cazul în care - partea dreaptă a ecuației i-lea. Această relație va fi efectuată indiferent de decizie, în cazul în care este necesar:

Din prima ecuație obținem:

După găsirea și coeficienții progonochnyh. folosind ecuația (1), pentru a obține soluția sistemului. În același timp,

interpolare spline este bun, deoarece necesită cunoașterea doar nodurile funcției, dar nu și derivații săi [34, 36, 43].