Antiderivatives

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Cifra reprezintă un grafic al unei funcții y = F (x) - una dintre primitivelor unei funcții oarecare (x) f. definită pe intervalul (-5, 5). Folosind modelul, se determină numărul de soluții ale ecuației f (x) = 0 în intervalul [-3; 4].

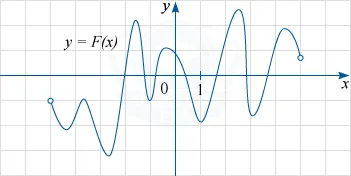
Conform definiției primitive, egalitatea: F „(x) = f (x). De aceea, ecuația f (x) = 0 poate fi scris sub forma F „(x) = 0. Așa cum este ilustrat în Figura graficul y = F (x), este necesar să se găsească punctele din intervalul [-3; 4], în care derivata funcției F (x) este zero. Figura arată că acest lucru se va abscisă puncte extreme (maxim sau minim) ale graficului F (x). în interval lor a spus exact 7 (patru puncte de minim și maxim trei puncte).

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Cifra reprezintă un grafic al unei y funcției = f (x) (care este o linie întreruptă compusă din trei segmente rectilinii). Folosind modelul, calcula F (5) -F (0), unde F (x) - una din funcția primitivelor f (x).

Conform formulei diferenței Teorema fundamentală F (5) -F (0), unde F (x) - una din funcția primitivelor f (x), egală cu suprafața trapezului curbat delimitate funcție orar y = f (x), y = 0 drepte , x = 5 și x = 0. Din grafic determinăm care a spus trapez curbilinie este un trapez cu o bază egală cu 5 și 3 și o înălțime de 3.

Suprafața sa este egală cu \ frac \ cdot 3 = 12.

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Cifra reprezintă un grafic al unei funcții y = F (x) - una dintre primitivele unei anumite funcții f (x), definit pe intervalul (-5, 4). Folosind modelul, se determină numărul de soluții ale ecuației f (x) = 0 în intervalul (-3, 3].

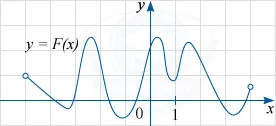
Conform definiției primitive, egalitatea: F „(x) = f (x). De aceea, ecuația f (x) = 0 poate fi scris sub forma F „(x) = 0. Așa cum este ilustrat în Figura graficul y = F (x), este necesar să se găsească punctele din intervalul [-3; 3], în care derivata funcției F (x) este zero.

Figura arată că acest lucru se va abscisă puncte extreme (maxim sau minim) ale graficului F (x). în interval lor a spus exact 5 (două puncte de minim și maxim trei puncte).

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Figura arată un grafic al unei y funcției = f (x). Funcția F (x) = - x ^ 3 + 4,5x ^ 2-7 - una dintre primitivele funcției f (x).

Găsiți zona figura umbrită.

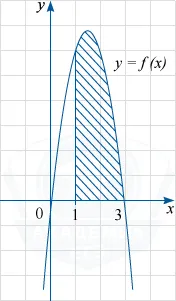
Cifra hașurată este trapezoid curbat delimitat deasupra graficului y = f (x), linii drepte y = 0, x = 1 și x = 3. Conform formulei Teorema fundamentală a zonei sale S este egal cu diferența dintre F (3) -F (1), unde F (x) - subiectul menționat funcția primitivă f (x). Prin urmare, S = F (3) -F (1) = -3 ^ 3 + (4,5) \ cdot 3 ^ 2 -7 - (- 1 ^ 3 + (4,5) \ cdot 1 ^ 2 -7) = 6,5 - (- 3,5) = 10.

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Cifra reprezintă un grafic al unei y funcției = f (x). Funcția F (x) = x ^ 3 + 6x ^ 2 +-13x 5 - unul dintre primitivele funcției f (x). Găsiți zona figura umbrită.

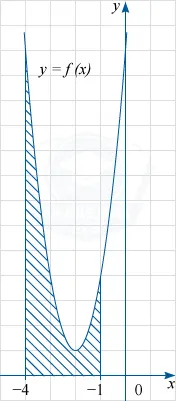
Cifra umbrită este trapezoid curbată delimitată de graficul y = f (x) și linii drepte y = 0, x = -4 și x = -1. Conform formulei Teorema fundamentală a zonei sale S este egal cu diferența dintre F (-1) -F (-4), unde F (x) - subiectul menționat funcția primitivă f (x).

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Figura arată un grafic al unei y funcției = f (x). Funcția F (x) = x ^ 3 + 18x ^ 2 + 221x- \ frac12 - una dintre primitivele funcției f (x). Găsiți zona figura umbrită.

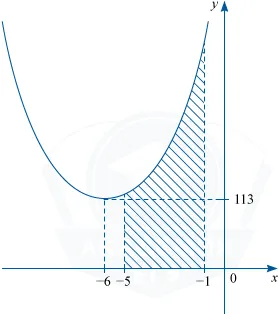
Prin formula Teorema fundamentală S = F (-1) -F (-5).

F (-1) = (-1) ^ 3 + 18 \ cdot (-1) ^ 2 + 221 \ cdot (-1) - \ frac12 = -204- \ frac12.

F (-5) = (-5) ^ 3 + 18 \ cdot (-5) ^ 2 + 221 \ cdot (-5) - \ frac12 = -125 + 450-1105- \ frac12 = -780- \ frac12.

F (-1) -F (-5) = -204- \ frac12- \ stânga (-780- \ frac12 \ dreapta) = 576.

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

Figura arată un grafic al unei y funcției = f (x). Folosind modelul, calcula F (9) -F (3), unde F (x) - una din funcția primitivelor f (x).

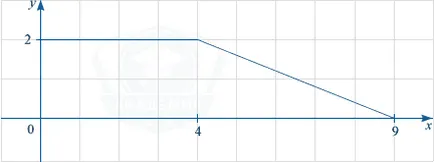
F (9) -F (3) = S. unde S - suprafața figurii delimitate de graficul unei y funcției = f (x), linii drepte y = 0 și x = 3, \ = 9 x. Luați în considerare figura de mai jos.

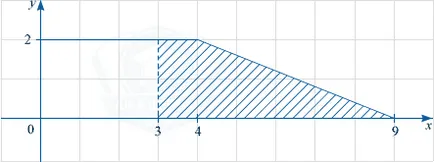
Această cifră - trapez cu bazele 6 și 1 și 2. Înălțimea sa este egală cu zona \ Frac \ cdot2 = 7.

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

In graficul unei y funcției = f (x) prezintă un plan de coordonate. Unul dintre primitivelor acestei funcții are forma: F (x) = - \ frac13x ^ 3- \ frac52x ^ 2-4x + 2. Găsiți zona figura umbrită.

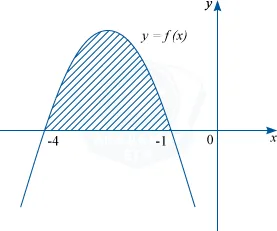
Figura arată că cifra eclozat delimitate la punctele abscisă -4, -1. iar graficul ordonata a funcției: f (x). Deci, zona a figurii, putem găsi diferența folosind valorile primitive la punctele de -1 și -4. conform formulei unei integrale definitive:

Membru supleant valoarea condițiilor primitive și de a obține aria figurii:

Tipul de locuri de muncă: 7
Subiect: Funcțiile primitive

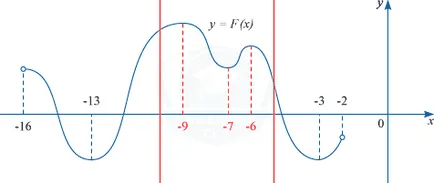
Primitiv y = F (x) a unei y funcției = f (x) este definit pe intervalul (-16, -2). Se determină cât de multe soluții a ecuației f (x) = 0 în intervalul [-10; -5].

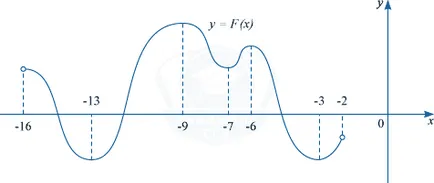
Formula primitiv este următoarea:

Conform problemei pentru a găsi punctul în care funcția f (x) este zero. Luând în considerare formula primitivă, ceea ce înseamnă că trebuie să găsiți punctul în care F „(x) = 0. adică punctele la care derivata primitiv este zero.

Știm că derivatul este zero, la punctele de extremă locale, și anume, Funcția are soluții în acele puncte în care creșterea F (x) este înlocuită cu descreșterea și vice-versa.

In intervalul [-10; -5] se poate observa că acest punct: -9; -7; -6. Prin urmare, ecuația f (x) = 0 are trei soluții.