accesibilități matrice - studopediya

Graficul nod este numit de atins vârful graficului, în cazul în care există cel puțin o cale de la.

Setul de noduri R (vi). accesibil de la unele noduri. Acesta este dat de:

Într-adevăr, primul element al setului este un nod. care este accesibilă de la sine, prin calea de lungime zero; G (vi) - setul de vârfuri vj. vi realizabile la folosirea căilor de lungime unul; T 2 (vi) - o multitudine de noduri accesibile din vi folosind lungimea celor două căi; - o multitudine de noduri de la p vi accesibil folosind lungimea drumului. Astfel, setul R (vi) este obținut prin realizarea secvențială operația de îmbinare de la stânga la dreapta în expresia (2.9), atâta timp cât puterea de setul curent nu încetează să crească la următoarea operație de îmbinare. Din acest punct operațiunile ulterioare nu vor da asocierea unor noi elemente la set R (vi). Numărul de organizații care au nevoie pentru a efectua depinde de graficul G. Cu toate acestea, în cazul în care graficul este finit, atunci p

matrice accesibilități se numește o matrice pătrată de ordinul n. care elementul

Exemplu. Construi o matrice a graficului accesibilități G, prezentat în Fig. 2.6.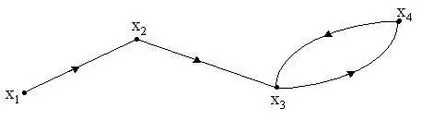

Prin urmare, matricea accesibilități are forma:

Este evident că elementele di, i = 1, i = 1, 2, ..., n, fiecare vârf este accesibil de la sine.

matrice kontrdostizhimostey (invers accesibil) este definit după cum urmează:

unde Q (vi) - setul de vârfuri vi ÎV. că fiecare nod al acestui set poate ajunge în partea de sus a vi:

în care: - o multitudine de noduri, dintre care vârful este realizabil folosind lungimea căii vi unitate; ) - o multitudine de noduri, vârful care este realizabil vi folosind o lungime de cale a doua, etc. funcționare a Uniunii în expresia (2.10), de la stânga la dreapta, atâta timp cât o altă asociație nu mai schimba „setul curent“.

Exemplu. Construirea unui kontrdostizhimostey matrice Q pentru G Fig. 2.6.

Matricea kontrdostizhimostey va arata:

Din definiția D matricei și Q, rezultă că Q = D T. Deoarece D (vi) este un set de noduri accesibil de la. și Q (vj) - o multitudine de noduri, dintre care vârful este vj realizabil. atunci D (vi) - o multitudine de noduri, fiecare dintre acestea aparține cel puțin o cale de rulare de la vi la vj. Aceste vârfuri sunt numite esențiale (indispensabile) în raport cu cele două vârfuri vi capăt și vj. Nodurile sunt numite neesențial (excesivă), deoarece îndepărtarea lor nu afectează calea de la VI la vj.