4-4 Curbe parametrice
Forma parametrică fiecare punct de coordonate pe curba reprezentată în funcție de un parametru. Parametrul specifică vectorul de coordonate al punctului de pe curba. Pentru două dimensionale puncte parametru curbă coordonate sunt:
Apoi, reprezentarea vectorială a punctului de pe curba:
Pentru a obține forma non-parametrică, ar trebui excluse din cele două ecuații și să aducă una în termenii și.
Formularul Parametric vă permite să-și prezinte închis evaluate și curbe. , Adică. E. Vectorul tangent Derivative, acolo
unde „denotă o diferențiere în ceea ce privește un parametru. Panta curbei, este egală cu
Rețineți că, atunci când panta este infinit. Reprezentarea parametrică nu este în acest caz, dificultățile de calcul suficient pentru a egala cu zero, o componentă a vectorului tangent.
Deoarece valoarea punctului numai a parametrului este determinat pe o curbă parametrică, această formă este independentă de sistemul de coordonate. Obiective și lungimea curbei sunt determinate de intervalul de schimbare a parametrului. Acesta este adesea convenabil de a normaliza parametrul de interes în segmentul curbei la. Osenezavisimost curba parametric face ușor de transportat cu ea transformarea afină discutată în secțiunea. 2 și 3.
Cea mai simplă reprezentare parametrice în linie dreaptă. Pentru cei doi vectori de poziție și formă parametrică a unui segment de dreaptă între ele este următoarea:
Deoarece este un vector, fiecare componentă are reprezentarea parametric și între:
Exemplul 4-1 Reprezentarea parametrică a unei linii drepte
Găsiți o reprezentare parametrică a segmentului între punctele și vectorul tangent și pantei. Reprezentarea parametrică:
Reprezentarea parametrică a elementelor constitutive și:
Diferențierea, obținem un vector tangent:
unde - vectorul tangent, o, - vectorii unitare respectiv direcțiile.
Inclinarea segmentului este egal cu
Fig. 4.3 comparat reprezentarea neparametrică și parametrică a unui cerc în primul cadran. vizionări neparametrici
este prezentată în Fig. Și 4.3.
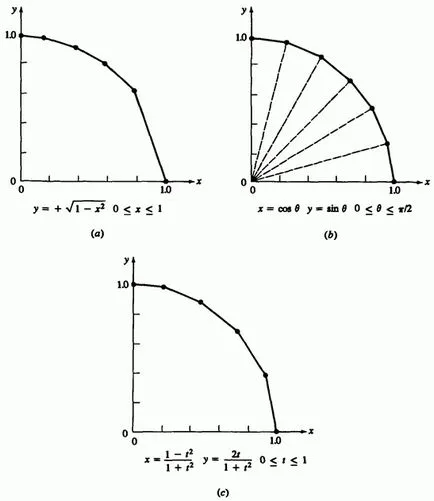
Fig. 4-3 Introducere Circumferința primul cadran.
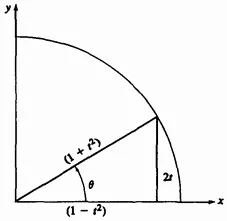
Fig. 4-4 Comunicarea între reprezentarea parametrica.
Punctele de pe arc corespund cu creșteri egale. Când acest arc este compus din segmente de lungime diferită, și a obținut o reprezentare grafică foarte aproximativă a cercului. În plus, calculul rădăcinii pătrate - o operațiune de computațional scump.
formă parametrică standard a unității cercului:
unde parametrul - unghiul geometric, măsurat în sens antiorar din jumătatea pozitivă. Fig. 3.4b arată arc construit prin creșteri egale în intervalul de parametri. Punctele sunt situate la aceeași distanță de-a lungul circumferința unui cerc și arată mult mai bine. Dezavantajul acestei reprezentări - complexitatea calculului funcțiilor trigonometrice. (O metodă mai simplă este discutată mai jos în Sec. 4.5).
Reprezentarea parametrica a curbei nu este singurul exemplu,
reprezintă, de asemenea, un arc al cercului unitate în primul cadran (Fig. 4.3s). Relația dintre reprezentarea parametrica (3.4) și o reprezentare parametrică etalon (4.2) este prezentată în Fig. 4.4. Se poate observa că pentru cercul unitate
Faptul că ecuația 4.3 reprezintă un singur arc de circumferință, este susținută de următoarele:
în cazul în care - o singură rază.
Fig. 4-3s arată rezultatul pentru creșteri egale. El este mai bună decât în mod explicit (4-1), dar mai rău decât cea a unei reprezentări parametrice standard (4-2). Cu toate acestea, ecuația (4-3) este mai ușor din punct de vedere computational, și anume, Această soluție de compromis.
Exemplu 4-2 Determinarea punctelor pe o curbă parametrică
Lăsați este necesar să se găsească valoarea specificată. De exemplu, să presupunem că și este nevoie pentru a calcula cercul unitate. Pentru reprezentarea explicită (4-1) calculat direct:
Pentru prima reprezentare parametrică trebuie exprimată printr-un parametru, apoi utilizați valorile rezultate pentru a găsi. Reprezentarea parametrică a ecuației (4-2)
Pe de altă parte, din ecuația 4-3
Noi rezolva primul dintre aceste ecuații în ceea ce privește
În cazul reprezentării parametrice mai complexe este mai convenabil să caute valoarea variabilei metode iterative explicite.
Reprezentarea parametrica a secțiunilor conice osenezavisimo și oferă o calitate a imaginii mai bună decât neparametrică; Cu toate acestea, ambele au avantajele și dezavantajele lor și sunt adesea folosite în grafica pe calculator.