zona poligon
Putem spune că aria unui poligon - o valoare care indică partea a planului ocupat de poligon. Per măsurare unitatea de suprafață luând o suprafață pătrată cu o \ laterală (1 \) cm \ (1 \) mm etc. (Pătrat unitate). Apoi zona va fi masurata in cm \ (^ 2 \). mm \ (^ 2 \), respectiv.
Cu alte cuvinte, putem spune că zona din cifra - este valoarea, valoarea numerică care indică de câte ori pătrat unitate se potrivește în această figură.
1. Zona oricărui poligon - o valoare pozitivă.
2. poligoane de șanse au zone egale.
3. În cazul în care un poligon compus din mai multe poligoane, suprafața este egală cu suma suprafețelor acestor poligoane.
4. Suprafața unui pătrat de latură \ (a \) este \ (a ^ 2 \).
Teorema: aria unui dreptunghi
Suprafața unui dreptunghi cu laturile \ (a \) și \ (b \) este egal cu \ (S = ab \).
Terminati dreptunghi \ (ABCD \) la pătratul \ (a + b \). așa cum se arată mai jos:

Acest pătrat este un dreptunghi de \ (ABCD \). un alt egal cu el dreptunghi și două pătrate cu laturi \ (a \) și \ (b \). Astfel,
Înălțimea paralelogram - perpendiculara trasată de vertexul spre partea paralelogram (sau să continue mâna) care nu conține acest nod.
De exemplu, înălțimea \ (BK \) cade pe partea \ (AD \). și înălțimea \ (BH \) - continuarea părților \ (CD \):
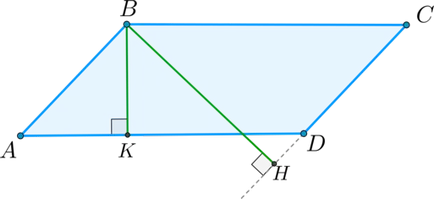
Teorema: aria unui paralelogram
Suprafața unui paralelogram este egală cu produsul dintre înălțimea părților la care această înălțime se realizează.
Desenați perpendicularele \ (AB '\) și \ (DC' \). așa cum se arată în figură. Rețineți că aceste perpendicularele sunt egale cu înălțimea paralelogram \ (ABCD \).

Apoi, \ (AB'C'D \) - un dreptunghi, prin urmare, \ (S_ = AB „\ cdot AD \).
Rețineți că triunghiurile unghi drept \ (ABB '\) și \ (DCC' \) sunt egale. Astfel,
Vom numi partea căreia triunghiul a avut loc înălțimea bazei triunghiului.
Suprafața unui triunghi este egală cu jumătate din produsul de bază și înălțimea, realizată de această fundație.
Să \ (S \) - Triangle pătrat \ (ABC \). Noi luăm direcția de \ (AB \) de la baza triunghiului și trage înălțimea \ (CH \). Vom arăta că \ finisaj triunghi \ (ABC \) la paralelogram \ (ABDC \) așa cum se arată mai jos [S = \ dfracAB \ cdot CH \.]:
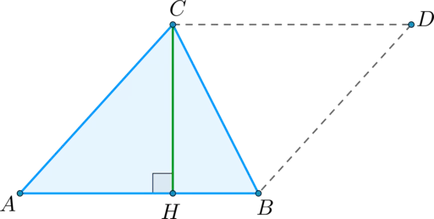
Triunghiuri \ (ABC \) și \ (DCB \) sunt pe trei laturi (\ (BC \) - partea lor comună, \ (AB = CD \) și \ (AC = BD \) ca partea opusă a paralelogram \ (ABDC \ )), astfel încât zonele lor sunt egale. Prin urmare, zona \ (S \) triunghi \ (ABC \) este egal cu jumătate din aria paralelogramului \ (ABDC \). adică \ (S = \ dfracAB \ cdot CH \).
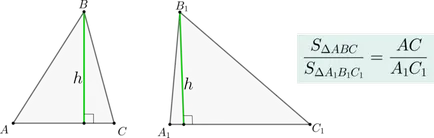
Dacă două triunghiuri \ (\ triunghiul ABC \) și \ (\ triunghi A_1B_1C_1 \) au aceeași înălțime, zona lor de interes ca bază la care altitudinea făcută.
Mediana unui triunghi se împarte în două triunghiuri de suprafață egală.
Dacă două triunghiuri \ (\ triunghi ABC \) și \ (\ triunghi A_2B_2C_2 \) au fiecare un drept egal, ele sunt ca o zonă de lucru din laturile care formează colțul.
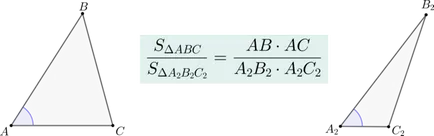
Să \ (\ unghi A = \ unghiul A_2 \). Compatibil aceste unghiuri așa cum se arată (punctul \ (A \) este aliniată cu punctul \ (A_2 \)):
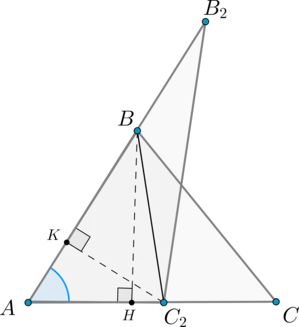
Desenați înălțime \ (BH \) și \ (C_2K \).
Triunghiuri \ (AB_2C_2 \) și \ (ABC_2 \) au aceeași înălțime \ (C_2K \). Prin urmare: \ [\ dfrac >> = \ dfrac \]
Triunghiuri \ (ABC_2 \) și \ (ABC \) au aceeași înălțime \ (BH \). Prin urmare: \ [\ dfrac >> = \ dfrac \]
Unghiulară-pătrat triunghi ipotenuza lungime egală cu suma pătratelor lungimilor picioarelor:

Invers, dacă triunghiul pătrat lungime de o parte egală cu suma pătratelor lungimilor celorlalte două părți, un triunghi dreptunghic.
Zona unui triunghi dreptunghic este egală cu jumătate din muncă picioare.
Teorema: Formula Heron
Să \ (p \) - Triangle semiperimetrul, \ (un \). \ (B \). \ (C \) - lungimea laturilor sale, în timp ce zona sa este \ [S _ = \ sqrt \]pentru că romburi este un paralelogram, este adevărat, aceeași formulă pentru ea, și anume, Zona romburi este egală cu produsul dintre înălțimea părților la care această înălțime se realizează.
Aria unui patrulater convex, diagonala care este perpendiculară, egală cu jumătate din produsul diagonalelor.
Luați în considerare patrulaterul \ (ABCD \). Să \ (AO = a, CO = b, BO = x, DO = y \):
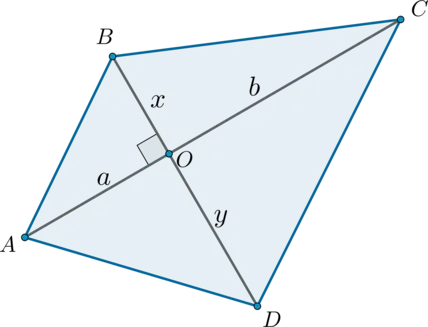
Rețineți că acest dreptunghi este compus din patru triunghiuri în unghi drept, prin urmare, o suprafață egală cu suma suprafețelor de triunghiuri:
\ (\ Incepeți S _ = \ frac12ax + \ frac12xb + \ frac12by + \ frac12ay = \ frac12 (ax + xb + de + ay) = \\ \ frac12 ((a + b) x + (a + b) y) = \ frac12 (a + b) (x + y) \ end \)
Impact: Zona de romb
Suprafața rombul este egală cu jumătate din produsul diagonalelor: \ [S _> = \ dfrac12 d_1 \ cdot d_2 \]
Înălțimea trapez - perpendiculara trase din partea de sus a unei baze la o altă bază.
Teorema: aria trapezului
Zona de trapez este egală cu produsul jumătății totalul bazelor de sus.
Luați în considerare trapezoid \ (ABCD \) cu baze \ (BC \) și \ (AD \). Desenați \ (CD „\ paralel AB \). așa cum se arată mai jos:
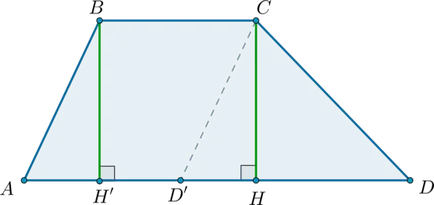
Apoi \ (ABCD „\) - un paralelogram.
Egal ca \ (BH '\ făptașul AD, CH \ făptașul AD \) (\ (BH' = CH \) - înălțimea trapezului).
Apoi \ (S_ = BH '\ cdot AD' = BH „\ cdot BC, \ quad S _ = \ dfrac12CH \ cdot D'D \)
pentru că trapez constă dintr-un paralelogram \ (ABCD '\) și triunghiul \ (CDD' \). că suprafața sa este egală cu suma suprafețelor paralelogramului și triunghiul, adică:
\ [S_ = S_ + S_ = BH '\ cdot BC + \ dfrac12CH \ cdot D'D = \ dfrac12CH \ stânga (2BC + D'D \ dreapta) = \] \ [= \ dfrac12 CH \ stânga (BC + AD' + D'D \ dreapta) = \ dfrac12 CH \ stânga (BC + AD \ dreapta) \]