Un număr de distribuție
În cursul secțiunii dedicate conceptele de bază ale teoriei probabilității, am introdus conceptul foarte important de variabile aleatoare. Aici vom da dezvoltarea în continuare a acestui concept și indică moduri în care variabilele aleatoare pot fi descrise și caracterizate.
După cum sa menționat deja, cantitatea aleatoare este o cantitate care este un rezultat al experienței poate lua una sau o altă valoare, nu este cunoscută în avans - care unul. De asemenea, am convenit să se facă distincția între velichinypreryvnogo aleatoare (discrete) și de tip continuu. Valorile posibile sunt valori discontinue pot fi enumerate în avans. Valorile posibile sunt valori continue pot fi enumerate în prealabil și umplute în mod continuu cu un anumit interval.
Exemple de variabile aleatoare continue:
1) numărul de apariții ale emblemei cu trei aruncări monede (valori posibile 0, 1, 2, 3);
2) frecvența apariției emblemei în același experiment (valori posibile);
3) numărul de elemente eșuate într-un dispozitiv format din cinci elemente (valori 0, 1, 2, 3, 4 posibile, 5);
4) numărul de rezultate pozitive într-un plan care este suficientă pentru a scoate din acțiune (valori posibile 1, 2, 3, ..., n, ...);
5) numărul de aeronave în lupta aer (doborâte valori posibile 0, 1, 2, ..., N, unde - numărul total de aeronave implicate în luptă).
Exemple de variabile aleatoare continue:
1) abscisă (ordonată) din punctul de impact cu împușcat;
2) distanța de la punctul de lovire în centrul țintei;
3) înălțimea contorului de eroare;
4) cănule uptime.
În cele ce urmează variabilele aleatoare notată în litere mari, și valorile lor posibile - corespunzătoare litere mici. De exemplu, - numărul de rezultate pentru trei fotografii; posibile valori.
Luați în considerare variabile aleatoare discontinue cu valori posibile. Fiecare dintre aceste valori este posibil, dar nu în mod semnificativ, iar variabila X poate lua fiecare dintre ele cu o anumită probabilitate. Ca urmare, valoarea X va experimenta una dintre aceste valori, adică apariția unuia din grupul plin de evenimente incompatibile:
Notăm probabilitatea acestor evenimente cu litere p indici relevanți:
Deoarece evenimentele incompatibile (5.1.1) formează un grup complet,
și anume suma probabilităților tuturor posibile variabile aleatoare este egală cu una dintre valori. Acest total veroyatnostkakim mod distribuit între valorile individuale. O variabilă aleatoare este descrisă în întregime de către punctul de vedere probabilistic, dacă ne întrebăm această distribuție, și anume, exact specifica care are probabil fiecare eveniment (5.1.1). În acest fel vom stabili așa-numita lege de distribuție a variabilei aleatoare.
legea aleatoare de distribuție valori este orice raport, stabilind relația dintre valorile posibile ale variabilei aleatoare și probabilitățile corespunzătoare. Despre variabila aleatoare, vom spune că se supune acestei legi de distribuție.
Stabilirea unui formular în care legea de distribuție variabilă aleatoare discontinuă poate fi setat. Cea mai simplă formă de sarcina legii este un tabel care listează valorile posibile znacheniyasluchaynoy și probabilități corespunzătoare:
Acest tabel va fi numit urmatoarea variabila aleatoare.
Pentru a da o distribuție număr de peste vedere grafică, de multe ori recurg la reprezentarea grafică a acesteia: pe axa abscisei valori posibile ale variabilei aleatoare, și axa ordonată - aceste valori de probabilitate. Pentru claritate, punctele de date sunt conectate prin segmente de linie. Această cifră se numește distribuție poligon (Fig. 5.1.1). distribuție Poligon, precum și numărul de distribuții caracterizează complet variabila aleatoare; este o formă de distribuție.
Uneori este convenabil așa-numita interpretare „mecanică“ a unui număr de distribuție. Să ne imaginăm că o anumită masă egală cu unitatea, este distribuit de-a lungul abscisa, astfel încât la punctele individuale, respectiv, concentrat în masă. Apoi, un număr de distribuție este interpretat ca un sistem de puncte materiale cu niște mase situate pe axa x.
Luați în considerare câteva exemple de variabile aleatoare continue cu legile de distribuție.
Exemplul 1 produce o experiență în care este posibil să primiți sau nu primesc evenimentul. Probabilitatea unui eveniment este de 0,3. Considerăm o valoare aleatoare - (. Adică, aleatoriu evenimentele caracteristice variabile care iau valoarea 1 în cazul în care este afișat și 0 dacă nu apare) numărul de apariții ale unui eveniment în acest experiment. Construct seria de distribuție și poligonului a distribuției.
Decizie. Valoarea are doar două valori, 0 și 1. Numărul de valori de distribuție este:
distribuția poligonal este prezentată în Fig. 5.1.2.
Exemplul 2 produce trei ardere shooter la o țintă. Probabilitatea de a lovi ținta cu fiecare lovitură este de 0,4. Pentru fiecare lovitură a marcat 5 puncte săgeată. Construirea seria de distribuție de puncte în relief.
Decizie. Notăm numărul de puncte de knock-out. Valorile posibile de mărime. .
Probabilitatea ca aceste valori sunt la o repetiție de experimente teorema:
Mai multe distribuție granulometrică este după cum urmează:
distribuția poligonal este prezentată în Fig. 5.1.3.
Exemplul 3: Probabilitatea de apariție a unui eveniment într-un experiment este. Acesta a produs un număr de studii independente, care continuă până la prima apariție a evenimentului. după care experimentele sunt terminate. variabilă aleatoare - numărul de încercări efectuate. Construi valoarea serie de distribuție.
Decizie. Valorile posibile de mărime. 1, 2, 3, ... (teoretic nu sunt restricționate). Pentru valoarea adoptată o valoare de 1, este necesar ca un eveniment a avut loc în primul experiment; probabilitatea este. Pentru o valoare a luat o valoare de 2, aveți nevoie pentru a experimenta primul eveniment nu apare, iar al doilea - a apărut; probabilitatea este. în cazul în care. etc. Mai multe distribuție granulometrică este după cum urmează:
Primele cinci ordonata distribuția poligonului pentru cazul prezentat în Fig. 5.1.4.
Exemplul 4. Trăgătorul este tragere la o țintă la primul contact, având patru cartușe de muniție. Veroyatnostpopadaniya la fiecare lovitură este 0.6. Construirea seria de distribuție de muniție, restul necheltuită.
Decizie. Valoarea aleatorie - numărul de cartușe necheltuite - are patru valori posibile: 0, 1, 2 și 3. Probabilitățile acestor valori sunt respectiv egale cu:
Mai multe distribuție granulometrică este după cum urmează:
distribuția poligonal este prezentată în Fig. 5.1.5.
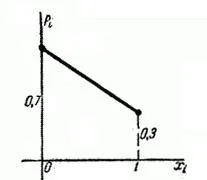
Exemplul 5. Dispozitiv tehnic poate fi utilizat în diferite circumstanțe și în funcție de aceasta, din când în când necesită ajustare. Pentru o singură utilizare a dispozitivului poate cădea la întâmplare în mod favorabil sau nefavorabil. Aparatul păstrează trei aplicații fără ajustare într-un mod favorabil; înainte de a patra trebuie să fie ajustat. În modul defavorizate, dispozitivul trebuie să fie ajustate după prima aplicare. Probabilitatea ca dispozitivul va beneficia de un tratament favorabil - 0,7, care, în nefavorabil - 0,3. Considerăm o valoare aleatoare - numărul de cereri pentru a regla dispozitivul. Construiți numărul de distribuție.
Decizie. O variabilă aleatoare are trei valori posibile: 1, 2 și 3. Probabilitatea ca. este probabilitatea ca primul dispozitiv de aplicare devine un mod nefavorabil, adică . Pentru o valoare valoare adoptată 2, este necesar ca primul aparat de aplicare are un mod favorabil, iar cel de-al doilea - în nefavorabile; probabilitatea de acest lucru. Că valoarea de valoare acceptată de 3, trebuie să primele două ori produsul a fost într-un tratament favorabil (după a treia oară, el va trebui în continuare să fie ajustate). Probabilitatea acestui fapt este.
Mai multe distribuție granulometrică este după cum urmează:
distribuția poligonal este prezentată în Fig. 5.1.6.
În n ° precedent, am introdus o serie de distribuție ca un răspuns cuprinzător (legea de distribuție) variabilă aleatoare discontinue. Cu toate acestea, această caracteristică nu este universală; ea există numai pentru variabilele aleatoare discontinue. Este ușor de observat că pentru valoarea nepreryvnoysluchaynoy a unor astfel de caracteristici nu pot fi construite. Într-adevăr, continuă velichinaimeet aleatoare număr infinit de valori posibile, umplând complet o anumită perioadă de timp (așa-numitul „set numărabil“). Creați un tabel care va lista toate valorile posibile ale unei variabile aleatoare, este imposibil. Mai mult decât atât, după cum se va vedea în continuare, fiecare valoare separată este o variabilă aleatoare continuă în mod normal, nu are nici o probabilitate nenulă. În consecință, pentru o variabilă aleatoare continuă, nu există nici o serie de distribuție în sensul că există pentru valoarea discontinuă. Cu toate acestea, diferite regiuni ale valorilor posibile ale variabilei aleatoare încă nu sunt la fel de probabil, și există o „probabilitate de distribuție“ pentru cantitatea continuă, deși nu în sens pentru ambele discontinuă.
Pentru a cuantifica caracteristicile distribuției de probabilitate este convenabil de a folosi un eveniment incredibil. și probabilitatea evenimentului. în cazul în care - o parte a variabilei curente. Veroyatnostetogo evenimente, evident, depinde. este o funcție de. Aceasta se numește o funcție de distribuție variabilă aleatoare și este notat cu:
Funcția de distribuție este uneori denumită funcția de distribuție cumulativă sau legea distribuției cumulative.
Funcția de distribuție - majoritatea caracteristicilor universale ale variabilelor aleatoare. Ea există pentru toate variabilele aleatoare: cum discontinuă și continuă. Funcția de distribuție este complet valoarea harakterizuetsluchaynuyu din punct de vedere probabilistic, și anume, Este o formă de distribuție.
Formulăm unele proprietăți generale ale funcției de distribuție.
1. Funcția de distribuție are o funcție descrescătoare a argumentului său, și anume, la.
2. În infinitate minus, funcția de distribuție este zero :.
3. În plus infinit, funcția de distribuție este egală cu un :.
Fără a da o dovadă riguroasă a acestor proprietăți, le ilustrează cu o interpretare geometrică vizuală. Pentru aceasta considerăm variabila aleatoare ca un punct aleatoriu pe axa x (fig. 5.2.1), care este un rezultat al experienței poate lua una sau o altă poziție. Apoi, funcția de distribuție estveroyatnost că un punct aleatoriu, ca urmare a experienței va obține punctul de stânga.
Vom crește. t. e. muta punctul spre dreapta pe axa orizontală. Evident, probabilitatea ca un punct aleatoriu cade la stânga. nu poate fi redusă; Prin urmare, funcția de distribuție cu creșterea scădere nu se poate.
Pentru a vă asigura că. Ne vom muta la infinit punctul spre stânga de-a lungul axei orizontale. Astfel de puncte de infiltrare accidentale la stânga, în limita devine eveniment imposibilă; naturale să-și asume chtoveroyatnost acest eveniment tinde la zero, și anume, .
În mod similar, fără a limita prin deplasarea punctului spre dreapta, vedem că. ca evenimentul devine semnificativ în limita.
Graficul funcției de distribuție, în cazul general, este un grafic funcție nondecreasing (Fig. 5.2.2), valorile care pornesc de la 0 și merg până la 1, în care la punctele discrete pot avea funcția de sare (discontinuități).
Cunoscând numărul de distribuție discontinuă a unei variabile aleatoare, putem construi cu ușurință această funcție de distribuție valoare. De fapt,
în cazul în care inegalitatea sub semnul însumare indică faptul că însumarea se extinde peste toate valorile. care sunt mai puțin.
În cazul în care variabila de curent trece prin unele dintre posibilele magnitudinea valorilor discontinue. Funcția de distribuție se schimbă brusc, iar magnitudinea salt este egal cu probabilitatea acestei valori.
Exemplul 1 produce o experiență în care este posibil să primiți sau nu primesc evenimentul. Probabilitatea unui eveniment este de 0,3. variabilă aleatoare - numărul de apariții ale evenimentului în experiența (valoarea intrinsecă a unui eveniment aleator). Pentru a construi funcția sa de distribuție.
Decizie. Mai multe distribuție granulometrică este după cum urmează:
Noi construim valoarea funcției de distribuție:
Graficul funcției de distribuție este prezentată în Fig. 5.2.3. Punctele de discontinuitate ia valori marcate cu puncte în figură (funcție continuă din stânga).
Exemplul 2. In condițiile din exemplul 4 experimente independente anterioare efectuate. Construirea funcția de distribuție a numărului de apariții ale evenimentului.
Decizie. Notăm - numărul de apariții ale evenimentului în patru experimente. Această valoare are un număr de distribuție
Am construi o funcție variabilă aleatoare:
Graficul funcției de distribuție este prezentată în Fig. 5.2.4.
Funcția de distribuție a oricărei variabile aleatoare discontinue este întotdeauna o funcție pas discontinua sare care are loc la punctul corespunzător valorilor posibile ale valorii aleatoare și ravnyveroyatnostyam aceste valori. Suma tuturor salturi funcției este egală cu unu.
Pe măsură ce numărul de valori posibile ale variabilei aleatoare și pentru a reduce intervalele dintre salturi devine mai mare, și se sare - mai puțin; Curba de viteză devine mai lină (Figura 5.2.5.); Variabile aleatoare se apropie treptat valoarea continuă, iar funcția sa de distribuție - (. Figura 5.2.6) la o funcție continuă.
În practică, de obicei, o funcție continuă a variabilei aleatoare este o funcție care este continuă la toate punctele, așa cum se arată în Fig. 5.2.6. Cu toate acestea, este posibil să se construiască exemple de variabile aleatoare, ale căror valori posibile sunt umplute în mod continuu cu un anumit interval de timp, dar pentru care funcția de distribuție nu este întotdeauna continuă și la punctele izolate discontinue (Fig. 5.2.7).
Astfel de valori aleatoare numite mixte. Ca un exemplu de valori mixte pot cauza daune zona, bomba țintă de depunere a cărui rază este egală cu ravagiilor R (Fig. 5.2.8).
Valorile variabilei aleatoare umple în mod continuu diferența între 0. se efectuează la pozițiile de tip bombă I și II, au o anumită probabilitate finită, iar aceste valori corespund salturi ale funcției de distribuție, în timp ce valorile intermediare (de tip poziția III) de distribuție este continuă. Un alt exemplu de variabilă aleatoare mixt - time dispozitiv T uptime testat în timpul t. Funcția de distribuție a variabilei aleatoare este continuă pretutindeni, cu excepția la punctul t.