Teorema de schimbare a energiei cinetice a sistemului mecanic - studopediya

Forma diferențială. Diferentialul energiei cinetice a punctului material este egală cu unitatea de forța care acționează asupra punctului,

Integral formă (final). Teorema energiei cinetice a punctului material al schimbării: variația energiei cinetice a unui punct material pe o mișcare ei egală cu suma algebrică a activității tuturor active la acest punct de forțe pe aceeași mișcare.

Teorema de schimbare a energiei cinetice a sistemului mecanic este formulat: variația energiei cinetice a sistemului mecanic în timp ce trece de la o poziție la alta este egală cu suma activității tuturor cul intern și extern atașat la sistem, această mișcare:

În cazul sistemului neschimbat volumul de muncă al forțelor interne în orice mișcare este zero (), atunci

Legea conservării energiei mecanice. Atunci când conduceți un sistem mecanic, ca răspuns la forțele care au un potențial de schimbare a energiei cinetice a sistemului de dependențe determinate de:

Suma de energie cinetică și potențială a sistemului este numită energia mecanică totală a sistemului.

Astfel. mișcarea unui sistem mecanic într-un câmp potențial staționar al energiei mecanice totale a sistemului în timpul mișcării rămâne neschimbată.

Sarcină. Sistem mecanic sub acțiunea gravitației în mișcare de la oprire. frecare Dat fiind corpul 3 de alunecare, neglijând alte forțe de rezistență și mase filamente, destinate inextensibil, determină viteza și accelerația corpului 1 în momentul în care au traversat calea devine egală cu s (fig. 3.70).

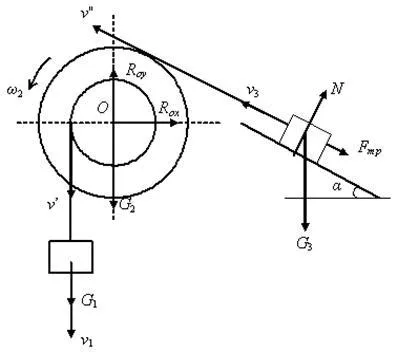
Decizie. Sistemul mecanic este supus unor forțe active ale ,. Aplicând liberarea principiu din sistemul de comunicație, arată reacție fix balama suport 2 și suprafața înclinată înăsprită. Vitezele de direcție ale organelor sistemului reprezintă, dat fiind faptul că corpul 1 coboară.

Rezolva problema, aplicând teorema de schimbare a energiei cinetice a sistemului mecanic:

unde T și - energia cinetică a sistemului în pozițiile inițiale și finale; - suma algebrică a forțelor exterioare aplicate sistemului pentru a muta sistemul din poziția inițială în finală; - volumul de muncă un sistem de forțe interne în aceeași mișcare.

Pentru sistemul considerat format din corpuri rigide conectate prin fire extensibile:

Deoarece poziția inițială a sistemului este în repaus, atunci. Prin urmare:

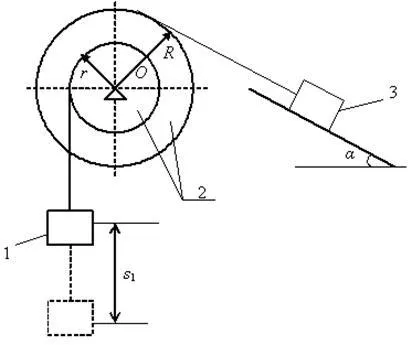
Energia cinetică a sistemului este suma energiei cinetice a organismelor 1, 2 și 3:

Energia cinetică a sarcinii 1, se deplasează în mod constant, este:

Energia cinetică a blocului 2, se rotește în jurul axei Oz. perpendicular pe planul desenului:

Energia cinetică a corpului 3 în mișcarea sa progresivă:

Expresia energiei cinetice conține viteze necunoscute ale tuturor organelor sistemului. Începeți cu definiția este necesară. Scapă de necunoscutele redundante, ajungând la ecuațiile de constrângere.

Ecuațiile de constrângere nu este altceva decât relațiile cinematice dintre vitezele și deplasările de puncte ale sistemului. În compilarea ecuațiile de constrângere exprimă tot sistemul de viteza de deplasare și necunoscută a corpurilor în mișcare prin viteza și sarcina 1.

Viteza de orice punct al jantei este egală cu viteza de corp rază mică de 1 precum și produsul a vitezei unghiulare a corpului 2 și raza r rotație:

Prin urmare, ne exprimăm viteza unghiulară a corpului 2:

Viteza de rotație a oricărui punct al unității jantei de rază mare, pe de o parte, egală cu produsul dintre viteza unghiulară și raza rotației blocului, iar celălalt - viteza corp 3:

Substituind valoarea vitezei unghiulare, obținem:

Integrarea condițiile inițiale ale (a) și (b), putem scrie raportul dintre punctele de deplasare ale sistemului:

Cunoscând vitezele în funcție de puncte de bază ale sistemului, înapoi la energia cinetică a expresiei și substituirea ecuației cu acestea (a) și (b):

Momentul de inerție al corpului 2 este egal cu:

Substituind valorile corpurilor de masă și momentul de inerție al corpului 2, putem scrie:

Determinarea cantității de muncă a tuturor forțelor externe ale sistemului la o anumită deplasare.

Forța de muncă de greutate 1

Forța de muncă este zero, deoarece aceste forțe sunt aplicate la punctul fix.

Forța de muncă de gravitate 3

Normal de lucru de reacție a corpului 3 este zero, pentru că forța este perpendiculară pe direcția de deplasare

Lucrul mecanic de frecare de alunecare

Valoarea lucrărilor efectuate de către forțe externe

Substituind valorile organelor de masă, deplasarea (a) și parametrii numerici, putem scrie:

Acum, în conformitate cu teorema de schimbare a energiei cinetice a sistemului mecanic și echivala valorile T

1 Viteza de corp obținută din expresia (g)

accelerare a corpului 1 poate fi determinată prin diferențierea ecuația timpului (g):