Statistică matematică 2, rezolvarea în matematică și așa mai departe problema.

1. În studiul structurii băncilor comerciale declarate de capital autorizat de trei mii de bănci din țară au fost selectate de către sistemul în sine un eșantion aleatoriu de o sută de repetiție fără. Datele privind distribuția băncilor pe această bază sunt prezentate în tabelul de mai jos:

A) probabilitatea ca dimensiunea medie a capitalului social al tuturor băncilor comerciale diferă de media dimensiunii sale în eșantion nu este mai mult de cinci milioane de ruble (în valoare absolută);

B) cantitatea de probă-repetiție liberă, în care aceeași abaterea de dimensiunea medie a capitalului social al tuturor băncilor (nu mai mult de cinci milioane de ruble a se vedea punctul. A)), poate fi asigurată cu o probabilitate de 0,95.

a) Găsiți dimensiunea medie a capitalului social, conform mediei ponderate cu formula:

Deviația standard de reducere a costurilor procentuală:

Probabilitatea ca dimensiunea medie a capitalului social al tuturor băncilor comerciale diferă de media dimensiunii sale în eșantion nu este mai mult de cinci milioane de ruble:

. B) cantitatea de probă-repetiție liberă, în care aceeași abaterea de dimensiunea medie a capitalului social al tuturor băncilor (nu mai mult de cinci milioane de ruble a se vedea punctul a)), poate fi asigurată cu o probabilitate de 0,95:

Pentru 0,95. atunci

2. Conform sarcinii anterioare, trebuie:

A) un model care emite ipoteza aproximează distribuția empirică, alegeri în cunoștință de;

B) folosind # 967; 2 - criteriul Pearson, la un nivel de semnificație a = 0,05 pentru a testa ipoteza că o variabilă aleatoare X - dimensiunea fondului autorizat al unei distribuții normale.

Construiți o histogramă pe un desen și curba de distribuție normală empirică corespunzătoare.

Form tabelul auxiliar pentru a calcula frecvențele teoretice:

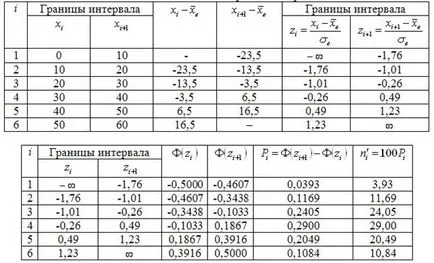
Să comparăm frecvențele empirice și teoretice:

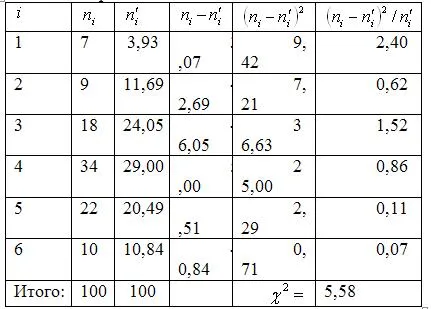
Prin tabelul de distribuție a punctelor critice # 967; 2 pentru nivelul de semnificație # 945; = 0,05 și numărul de grade de libertate. Valoarea calculată este mai mică decât masa, prin urmare, cu o probabilitate de 95% ar putea argumenta că variabila aleatoare X - dimensiunea fondurilor autorizate - distribuția normală.

Histograma distribuției empirice și curba normală corespunzătoare:

Pentru factorul 0,95 încredere este 1.96. atunci

Pentru a testa ipoteza egalității proporției de telespectatori sub 0.41 ipoteze concurente.

, atunci nu există nici un motiv pentru a respinge ipoteza nulă, adică, rezultatele sondajului nu sunt accidentale.

4. Distribuția cincizeci de companii din dimensiunile X active fixe (milioane de ruble) și producția y (milioane) date în tabelul de mai jos:

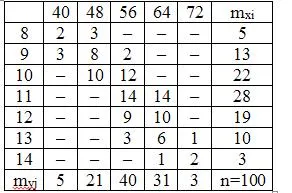
A) se calculează înseamnă gruparea și empiric construi linia de regresie;

B) presupunând că între variabilele X și Y, există o corelație liniară:

- găsi ecuația liniilor de regresie, pentru a construi graficele într-o singură figură cu liniile de regresie empirice și să dea interpretarea economică a ecuațiilor rezultate;

- calcula coeficientul de corelație, la un nivel de semnificație = 0.05 estimarea valorii și încheia conexiunea etanșeitate și direcția între variabilele X și Y;

- în cazul respingerii ipotezei absenței volumului producției de corelare de mărimea activelor fixe pentru a evalua măsura efectul dimensiunii mijloacelor fixe în valoare de ieșire (pentru a utiliza coeficientul de determinare și raportul de corelare);

-folosind ecuația de regresie corespunzătoare pentru a estima producția medie de întreprinderi, active fixe la 81 de milioane de ruble ..

Linia de regresie empirică a Y pe X:

Linia de regresie empirică a X pe Y:

Compune tabelul de decontare (pe linia de jos a lucrărilor):

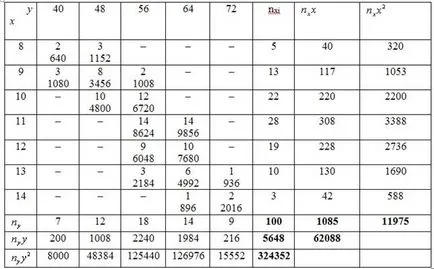
Am găsit media eșantionului: