Starea de echilibru a organismelor
echilibru al corpului se numește o stare în care orice accelerare a unui corp este egală cu zero, adică toate acțiunile pe forțele corpului și momentele sunt forțe echilibrate. În același timp, organismul poate:
- să fie într-o stare de liniște;
- mișcare uniformă în linie dreaptă;
- uniform se rotesc în jurul unei axe care trece prin centrul de greutate.
condiții de echilibru a corpului
În cazul în care organismul este în echilibru, cele două condiții sunt satisfăcute simultan.
- Suma vectorială a tuturor forțelor care acționează asupra unui corp este egal cu zero, vectorul: $ \ sum_n> _n> = \ overrightarrow $
- Suma algebrică a tuturor momentelor forțelor care acționează asupra unui corp este egal cu zero: $ \ sum_n = 0 $
Două condiții de echilibru sunt necesare, dar nu sunt suficiente. Aici este un exemplu. Luați în considerare rulare roata uniform fără să alunece pe suprafața orizontală. sunt îndeplinite ambele condiții de echilibru, cu toate acestea, corpul se mișcă.
Considerați cazul în care corpul nu se rotește. Pentru a se asigura că organismul nu se rotește și este în echilibru, este necesar ca suma proiecțiilor tuturor forțelor pe o axă arbitrară este egal cu zero, adică forța rezultantă. Apoi, corpul sau în liniște, sau se deplasează uniform într-o linie dreaptă.
Organismul, care are o axă de rotație, va fi în echilibru, dacă următoarea regulă cupluri de strângere: suma momentelor forțelor care se rotesc în sens orar a corpului, trebuie să fie egală cu suma momentelor forțelor care se rotesc în sens invers acelor de ceasornic.
Pentru a obține momentul potrivit, cu cel mai mic efort, forța care trebuie exercitată cât mai departe posibil de axa de rotație, crescând astfel brațul momentului și reducerea valorii forței, respectiv. Exemple de organisme care au o axă de rotație. pârghie, blocuri de usi, de foraj și așa mai departe.
Trei tipuri de echilibru al organismelor care au un punct de sprijin
- echilibru stabil, în cazul în care organismul este derivată din poziția de echilibru în poziția vecină în apropierea și lăsat în pace, revenirea la această poziție;
- echilibru instabil, atunci când organismul este derivată din poziția de echilibru într-o poziție adiacentă și lăsat în pace, vor fi mai mult să se abată de la această poziție;
- echilibru indiferent - atunci când organismul este derivată într-o poziție adiacentă și lăsat în pace, va rămâne în noua sa poziție.
corp Equilibrium cu o axă fixă de rotație
- rezistent în cazul în care poziția de echilibru, centrul de greutate ocupă poziția cea mai joasă a tuturor posibile dispoziții vecinii și energia potențială va avea cea mai mică valoare a tuturor valorilor posibile în poziții adiacente;
- instabilă, în cazul în care centrul de greutate are cea mai mare dintre toți vecinii prevederilor, iar energia potențială are o valoare maximă;
- indiferent, în cazul în care centrul de greutate C al corpului în toate pozițiile posibile ale vecinilor la același nivel, iar energia potențială la corpul de tranziție nu este schimbat.
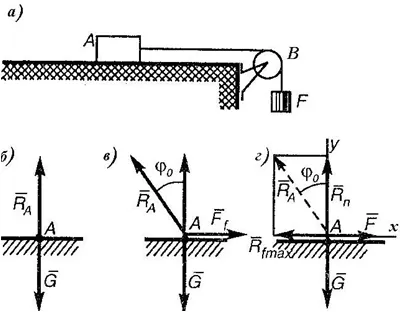
O masă corporală m = 8 kg livrate pe suprafața rugoasă a secțiunii orizontale. Pentru corp fir legat aruncat deasupra blocului B (Figura 1 a). Ce o sarcină F poate lega capătul firului, este suspendat din bloc, astfel încât să nu perturbe echilibrul corpului A? Coeficientul de frecare f = 0,4; bloc de frecare neglijabilă.
Definim greutatea corpului
G = mg = 8 $ \ cdot $ 9,81 = 78,5 N.
Noi credem că toate forțele sunt aplicate corpului A. Atunci când corpul este pus pe o suprafață plană, apoi acționează pe ea doar două forțe: (. Figura 1, b) greutatea G și de răspunsul opus RA suport direcție.
În cazul în care exercită o forță F, care acționează de-a lungul suprafeței orizontale, răspunsul RA, echilibrarea forțelor G și F, începe să se abată de la verticală, dar corpul A va fi în echilibru, atâta timp cât modulul de forță F nu depășește puterea maximă Rf frecare max corespunzătoare valorii de limitare a unghiului $$ o (Fig. 1c).
Extinderea răspunsului RA la cele două componente Rf max și Rn, obținem un sistem de patru forțe aplicate la același punct (Fig. 1d). Proiectând acest sistem de forțe pe x și axa y, obținem două ecuații de echilibru:
Rezolvăm sistemul de ecuații rezultat: F = Rf maxim, dar Rf max = f $ \ cdot $ Rn și Rn = G, deci F = f $ \ cdot $ G = 0,4 $ \ cdot $ 78,5 = 31,4 H; m = F / g = 31,4 / 9,81 = 3,2 kg.
R: greutatea sarcinii m = 3,2 kg