Soluție sisteme de inegalități liniare grafic
limitări ale sistemului de o astfel de problemă este inegalitatea în două variabile:
iar funcția obiectiv este dat de F = C1x + C2y. doriți să maximizați.
Răspunsurile la întrebarea: care pereche de numere (x, y) este o soluție a sistemului, și anume, satisfac fiecare dintre inegalitățile în același timp ..? Cu alte cuvinte, ceea ce înseamnă pentru a rezolva sistemul grafic?
Tu trebuie să înțeleagă mai întâi ce este soluția unei inegalitate liniară în două necunoscute.
Rezolva o inegalitate în două necunoscute - înseamnă să identifice toate perechile de valori necunoscute pentru care deține inegalitatea.
De exemplu, inegalitatea 3x - 5, y ≥ 42 satisface perechea (x y.). (100, 2); (3, -10), și așa mai departe. D. Sarcina este de a găsi toate perechile.
Luați în considerare următoarele două inegalități: ax + de către ≤ c. ax + de ≥ c. Direct ax + prin = c împarte planul în două jumătăți de plan, astfel încât coordonatele punctelor de una dintre ele satisfac ax + de> c. iar cealaltă inegalitate ax + + de
Pentru definiteness, să o lt 0, b> 0, c> 0. Toate punctele cu abscisa X0. situată deasupra P (de exemplu, punctul M) au ym> y0. și toate punctele situată sub punctul P. X0 abscisă. au yn 
Figura 1 semn Inegalitatea în a doua jumătate depinde de numărul a. b. c.
Aceasta implică următoarea metodă de sisteme grafice soluții de inegalități liniare în două variabile. Pentru a rezolva sistemul ar trebui:
- Pentru fiecare ecuație a scrie inegalitatea corespunzătoare acestei inegalități.
- Construiți o directă, este un grafic funcțiile definite de ecuații.
- Pentru fiecare linie pentru a determina semiplanul, care este definit de inegalitatea. Pentru a face acest lucru, să ia un punct arbitrar care nu se află pe o linie dreaptă, pentru a înlocui coordonatele sale în inegalitatea. dacă inegalitatea este adevărată, atunci semiplanul care conține punctul selectat, și o soluție de disparitate inițiale. În cazul în care o inegalitate incorectă, semiplanul pe de altă parte este un set de soluții directe ale inegalității.
- Pentru a rezolva sistemul de inegalități, este necesar să se găsească o zonă de intersecție a semiplanuri, care sunt soluția fiecărui sistem de inegalitate.
Această zonă poate fi gol, atunci sistemul de inegalități nu are nici o soluție, este inconsecventă. În caz contrar, se spune că sistemul este consecvent.
Pregătire poate fi un număr finit și infinit. Zona poate fi un poligon închis sau să fie nelimitată.
Să luăm în considerare trei exemple relevante.
Exemplul 1: rezolva grafic sistem:
x + y - 1 ≤ 0;
-2 x - 2y + 5 ≤ 0.
soluţie:
- ia în considerare ecuația x + y -1 = 0 și -2x - 2y + 5 = 0 inegalitățile corespunzătoare;
- construirea liniilor definite de aceste ecuații.

Figura 2
Noi definim cerut jumătate inegalitățile. Ia-un punct arbitrar, să (0, 0). Luați în considerare x + y- 1 0, înlocuind punctul (0, 0): 0 + 0 - 1, ≤ 0. Deci, în semiplanul care conține punctul (0, 0), x + y- 1 ≤ 0, te . semiplanul situată sub linie, este soluția primei inegalitate. Substituind punctul (0, 0), la un al doilea, se obține -2 # 8729; 0 - 2 # 8729; 0 + 5 ≤ 0, adică, în a doua jumătate în cazul în care punctul este (0, 0), -2x - 2y + 5≥ 0, și am întrebat unde -2x - 2y + 5 ≤ 0, și, prin urmare, la cealaltă jumătate-plan - aceea că, deasupra liniei.
Găsim intersecția acestor două jumătăți de avioane. Liniile sunt paralele, astfel încât planul nu se intersectează, făcând astfel sistemul inegalitățile de date nu are incompatibile.
Exemplul 2. Găsiți soluțiile grafice ale inegalităților:
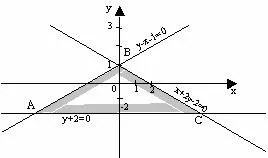
Figura 3
1. Scriem ecuațiile corespunzătoare inegalitățile și construi o linie dreaptă.
x + 2y - 2 = 0