Soluție aproximativă a ecuațiilor diferitelor instrumente

Tipul lecției: Învățarea și consolidarea noilor cunoștințe.

Tipul de activitate: lucrări practice cu calculatorul.

Durata: două lecții.

Obiectiv: Pentru a învăța să rezolve ecuații cu o anumită precizie la un interval predeterminat.

obiective:

• dezvoltarea cercetării, activitatea cognitivă a studenților;
• dezvoltarea abilităților de a folosi diverse instrumente software în rezolvarea unei probleme;
• dezvoltarea abilităților de comunicare ale elevilor.

Metode de predare: vizuale, cercetare, practic.

Software-ul:

1. Sistemul de operare Windows;
2. Microsoft Excel de la Microsoft pachet de birou;
3. Microsoft Visual Basic 6.0.

Plan de lecție:

1. Organizarea timpului.
2. Crearea unei situații problematice.
3. Folosind o metodă grafică pentru soluția aproximativă a ecuațiilor într-o foaie de calcul.
4. Studierea metodei de rezolvare a ecuațiilor de împărțire în două.
5. foaie de tablă Modelare pentru soluțiile aproximative ale metodei ecuației de împărțire în două.
6. Proiectul de simulare „soluție aproximativă“ la Visual Basic 6.0 limbaj orientat pe obiect.
7. experiment de calculator.
8. Analiza rezultatelor obținute.
9. Rezumând rezultatele lecției.

1. Organizarea timpului.

2. Crearea unei situații problemă.

- Astăzi, avem de a rezolva problema de a găsi rădăcini aproximative de cos (x) = x. folosind diverse instrumente software. Înregistrați subiectul lecției: „O soluție aproximativă a diferitelor instrumente.“

- Atâta timp cât nu știi nici tehnici matematice pentru a rezolva această ecuație, dar știi un program care poate rezolva aproximativ grafic. Care este programul? (Microsoft Excel).

3. Folosind o metodă grafică pentru soluția aproximativă a ecuațiilor într-o foaie de calcul.

- Care este sensul metodei? (Este necesar să se construiască un grafic al unei funcții y = cos (x) -X la un anumit interval, abscisa graficului punctelor de intersecție cu axa OX este rădăcina cos de ecuații (x) = x.)

- Ce trebuie să definiți pentru complot? (Lungimea în care există rădăcină).

- Fă-o metodă matematică. (. Setul de valori din partea stângă a ecuației, functia y = cos (x) este intervalul. [-1; 1] Prin urmare, ecuația poate avea rădăcina doar în acest interval.)

- Deci obține rădăcina aproximativă cos ecuația (x) = x în intervalul [-1; 1] cu un pas, de exemplu, 0,1 în Microsoft Excel.

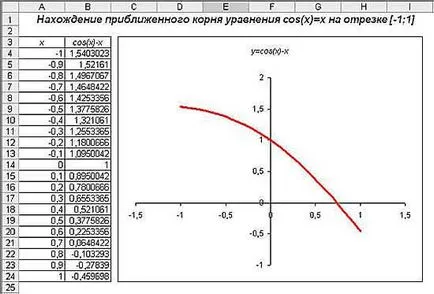
- rădăcină aproximativă x = 0,75. Cu toate acestea, această abordare nu are mare precizie. Pentru a găsi o ecuație aproximativă a rădăcinii cu respectivele metode matematice predeterminate utilizate în sus, în particular, metoda de împărțire în două.

4. Studiul metodei pentru rezolvarea ecuațiilor de împărțire în două.

Să considerăm o funcție f continuă (x), astfel încât rădăcina acestei ecuații este punctul de intersecție al graficului acestei funcții cu axa x.

Ideea metodei constă în reducerea de împărțire în două intervalul inițial [a; b], în care există o rădăcină a ecuației, segmentul specificat precizie h.

Procesul se reduce la împărțirea succesivă a segmentului jumătate litera c = (a + b) / 2 și aruncarea jumătate din segmentul ([a, c] sau [c; b]), care au o rădăcină. Segmentul selectat, capetele cărora funcția le asumă valori de semne opuse, adică produsul acestor valori este negativ. Funcția pe acest segment intersectează axa orizontală. Capetele acestui segment nou atribuite denumiri a, b.

Această diviziune continuă atâta timp cât lungimea segmentului este mai mică decât de două ori precizia, adică până când inegalitatea (b-a) / 2

(Imagine de afișare grafică obținută prin proiecție pe ecran, discuta despre ce trebuie ales segmente pentru o precizie de 0,5 Concluzie :. rădăcină aproximativă a x = 0,75 este găsit cu o precizie de 0,5.)

- Acum vom găsi rădăcina cos ecuația (x) = x la cel mai apropiat 0,001. Noi rezolva sarcina utilizând Microsoft Excel.

5. Modelarea foaie de calcul tabelar pentru soluțiile aproximative ale metodei ecuației de împărțire în două.

(Construcția aspectului tablă se realizează împreună cu elevii)

A cincea linie Valorile de scriere obținute după prima etapă, împărțirea în jumătate din segmentul inițial. În celula A5 și B5 trebuie să introduceți formula pentru determinarea limitelor noului segment. In celula C4, D4, E4, F4, formula G4 copiat din celulele C5, D5, E5, F5, G5, respectiv.

Astfel, în modul foaie, formulele de calcul tabelar iau forma următoare:

Apoi, va copia formula pe linia următoare, atâta timp cât coloana G apare valoarea dorită a rădăcinii.

6. Modelarea proiectului „soluție aproximativă“ la Visual Basic 6.0 limbaj orientat pe obiect.

(Construirea unui aspect formă și scrierea codului este efectuată de către elevi în mod independent: individual sau în grupuri)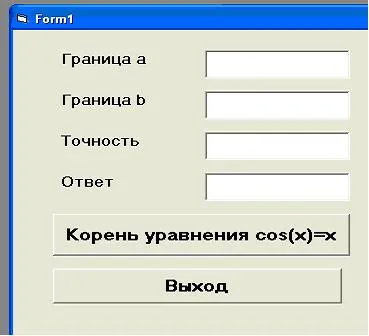

cod de program pentru rădăcină cos cheie ecuație (x) = x:

Private Sub Command1_Click ()