Soluția problemelor folosind proporții

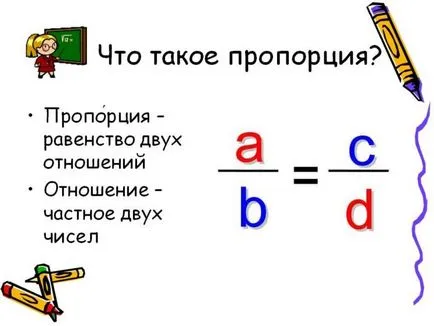
De multe ori, în practică, este necesar pentru a rezolva problema, care este cel mai eficient de a face cu proporții. În cazul în care există două condiții de valoare asociate, apoi pentru a rezolva această problemă este în mod convenabil conduce la egalitatea de fracțiuni. Fracțiunea se numește atitudine. De exemplu, o fracție sau 2: 3 - acest raport este de două până la trei. În cazul în care cele două rate egale între ele, vorbesc despre proporțiile. Ex. Dacă vom calcula valorile expresiile de pe stânga și dreapta „=“ semnul, poți fi sigur că acestea sunt egale. Acest lucru înseamnă că acestea sunt parte.
Egalitatea este exprimat în cuvinte, după cum urmează: „Zece se referă la cinci la 30 se referă la cincisprezece“ sau „Zece mai mult de cinci din același număr de ori treizeci și cincisprezece.“ Este evident că în figura 4 proporție valori numerice - 4 membri. Dacă oricare dintre ele nu este cunoscut, este posibil să se calculeze celelalte trei membri.

Pentru a calcula x, înmulțiți ambele fețe cu suficient 20:
Substituind valoarea pentru x și să verifice corectitudinea deciziei:
Partea dreaptă poate fi redusă la 4:
Astfel, la valoarea obținută x = 12, ecuație.
Înmulțim ambele părți prin:
Pentru a verifica valoarea substitut găsit în loc de x:
Partea din dreapta se reduce la 2:
Astfel, la calcularea valorii x = 6 egalitate adevărată.
Proprietatea principală a proporției
Dacă a: b = c: d, a și d sunt membri finali ai acestei proporții, b și c - mediu. Proprietatea principală este după cum urmează: produsul a membrilor extreme egală cu produsul de mediu: ad = bc. La înregistrarea în formă de egalitate și fracțiuni medii membri diagonale extreme 2 formă în formă de cruce a. Și proprietățile de bază pot fi din motive de claritate, formulate într-un alt mod: lucrările membrilor care alcătuiesc dreapta diagonala, este produsul dintre elementele ce formează stânga diagonală ( „regula Crucii“). Pentru a se asigura că această proprietate este de fapt inerent în proporții suficiente pentru a se multiplica ambele parti pe bd:
Reducerea ambelor părți pentru a scăpa de numitori și de a obține:
Folosind proprietatea principală, puteți găsi cu ușurință și rapid elementul necunoscut.
Prin proprietatea de bază:
Verificați corectitudinea deciziei:
Partea dreaptă a scăzut cu 5:
Astfel, atunci când valoarea rezultată a ecuației 40 x = true.
relație directă și inversă
Să presupunem că există două modificări parametrilor x și y. Mai mult decât atât, creșterea sau descreșterea în oricare dintre ele de mai multe ori duce la o astfel de schimbare, iar celălalt în același număr de ori. În acest caz vorbim de o relație directă, sau o proporționalitate directă între variabilele sunt: x este direct proporțională cu valoarea lui y, y este direct proporțională cu parametrul x. Sunt direct proporționale cu volumul de astfel de perechi de substanțe și masa sa, viteza și distanța parcursă de ceva timp, numărul de lucrători și volumul de muncă pe care ei sunt capabili de a efectua o anumită perioadă de timp, și așa mai departe. D.
Omul fuge de la casa lui la statia de autobuz (250 m), timp de 5 minute la autobuzul - în 7 minute. Care este distanța de la domiciliu până la stația de autobuz?
Deoarece creșterea timpului petrecut pe drum, este clar că a crescut și distanța parcursă. Mai mult, ambii parametri au crescut în același număr de ori: prima distanța până la al doilea raport este raportul dintre prima perioadă de timp pentru al doilea. Astfel, distanța și timpul pentru trecerea ei sunt direct proporționale între ele. Ne exprimăm problema fracțiilor ecuații și de a rezolva prin proprietățile principale:
Raspuns: distanta de la statia de autobuz este de 350 m
Să presupunem că există doi parametri variabile x și y. Mai mult decât atât, o creștere în oricare dintre ele de mai multe ori duce la o scădere în celălalt același număr de ori. Pe de altă parte, o scădere în oricare dintre ele orice număr de ori duce la o creștere în celălalt același număr de ori. Cu alte cuvinte, o creștere a unui parametru corespunzător unei creșteri a numărului invers alte perioade. În acest caz, se vorbește despre o relație inversă: x este invers proporțională cu y, y este invers proporțională cu x.
Sailing la o viteză de 45 km / h, barca a fost o cale scurtă de 4 ore. Cât timp va dura aceeași cale, la o viteză de 40 kilometri pe oră?
Pe măsură ce viteza de barca a scăzut, înot timp va dura mai mult. Prin urmare, viteza și timpul sunt invers proporționale între ele. Astfel, primul raport de viteză la al doilea raport este egal cu al doilea interval de timp pentru primul:
Răspuns: la o viteză de / h barca 40 km va trece în acest fel într-o oră.
Bob a completat numărul necesar de flotări timp de 1 minut. Vania este împins în jumătate din timp. De ceva timp, Ivan va apăsa cantitatea necesară de timp?
Deoarece Ivan este împins mai repede Vasey, cu atât mai puțin timp va dura. Mai mult decât atât, perioada Vanino de timp este la fel de multe ori mai mic decât numărul de ori mai mare decât viteza sa (în ori). Astfel, timpul de execuție a aceluiași număr de push-up-uri și de viteză sunt invers proporționale între ele. Notăm timp împinge Wani ca x, atunci
x = 1 min. = M
În ciuda existenței unei condiții de relație inversă, în acest caz, pentru decizia nu are sens să folosească egalitatea de fracțiuni.
