Soluția de ecuații cu parametrii

Lecția 2 ecuații pătratică cu parametri

Lectia 3 ecuații cu parametrii care trebuie rezolvate prin teorema Wyeth

Lecția 4 Rezolvarea problemelor cu parametri. Extreme.

Lectia 5 Rezolvarea problemelor cu parametri. Funcția.

Lecția 6 Soluția inegalităților cu parametri

Lecția 7 Soluție de ecuații cu parametrii

Lectia 8 sisteme de ecuații și inegalități

Lectia 10 ecuații cu parametri și module

Lecția 11 O ecuație exponențială cu un parametru

Lecția 12 ecuații trigonometrice cu un parametru

Lecția ecuația parametrului 13 Revenire

Lecția 14 Soluția ecuației cu parametrul folosind derivatul.

Lecția 15 Soluție grafică a ecuațiilor cu un parametru.

Lecția 16 inegalitate Irrational cu parametrul.

Lecția 17 Soluția modulului și parametrul folosind interpretarea geometrică.

Lecția 18 Principiul necesității și suficiență în rezolvarea problemelor cu parametri.

Lecția 19 Decizia inegalităților raționale cu un parametru.

Lecția 20 Soluția ecuației cu un parametru care conține rădăcina

Lecția Focus: ecuații liniare cu parametri.

Ecuațiile care conțin în plus față de ecuațiile necunoscute, și chiar valori literale sunt numite cu parametri. Structura matematică (sistem inegalitate ecuații, o pluralitate) care conține, în plus față de necunoscut, și mai multe valori alfabetice se numesc parametri de structură. De exemplu, ecuația AX = b este o ecuație liniară simplă, și în funcție de raportul dintre coeficienții a și b sunt trei cazuri posibile: dacă este zero și b este zero, iar dacă nu este egal cu zero și dacă este zero și b nu este zero. Acesta este de obicei luat în considerare două producții cu parametrii problemei. Prima scenă. Pentru fiecare valoare posibilă a parametrului sau a parametrilor pentru a găsi toate soluțiile predeterminate structura matematică, de exemplu, pentru a rezolva inegalitatea Hvostov 2 <1. Вторая постановка. Найти все значения параметра или параметров, при каждом из которых решение математической структуры удовлетворяет заданным условиям, например, найти все значения параметра а при которых система уравнений не имеет решений.

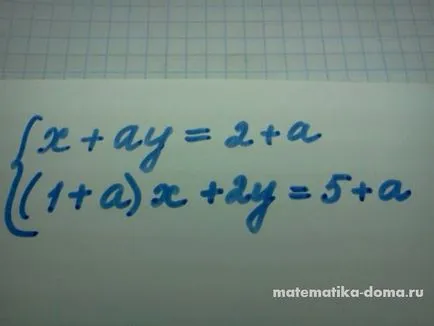
Complexitatea de rezolvare a structurilor matematice cu parametri este că o modificare a parametrului poate fi modificat nu numai coeficienții structurilor, dar și ODZ, și tipuri, metode și tehnici de soluții.

ecuații liniare cu parametri

ecuații liniare scrise în formă generală, este considerată ca o ecuație cu parametri, de exemplu, ah = b, unde x - necunoscut și, b este, parametrii așa-numitul. In general, orice ecuație pentru un anumit parametru sau valoarea de referință este cea la care dispare pentru un factor necunoscut.

În rezolvarea ecuației liniare cu parametru considerate cazuri în care parametrul este la o valoare deosebită pentru fiecare dintre ecuațiile și cele care diferă de la ea.

O valoare deosebită a parametrului și este în mod tipic valoarea unui = 0.

Luați în considerare soluția dintre ecuațiile următoare.

1. Rezolva ecuatia ax = b.