Soluția (conversie) a tabelului simplex on-line (de obicei, un dreptunghi) (decizia sarcinilor supreme

Considerăm în detaliu modul în care tabelele recalculat simplex (de exemplu, o singură iterație). Să fie un tabel simplex este prezentat în figura 1. Noi rezolva problema de maximizare a funcției obiectiv. Permițând coloana corespunde x2 variabile. și rezolvarea string x3 variabilă (numere roșii) la intersecția lor este de celule permisive (celule cu un fundal gri). Primul lucru pe care trebuie să facem - este de a înlocui variabila de bază. line Rezoluția arată care variabilă trebuie să fie derivat din baza (în acest caz, x3) și permițând coloanei arată care variabilă este de a intra în baza (în acest caz, x2). Fig.2 fapt înlocui variabila de bază este punctata de linia albastră.

Acum vom recalcula elementele care stau în rezoluția linie. Pur și simplu împărțiți fiecare dintre ele la un element permite (4 în exemplul nostru). Și toate elementele care permit coloana out zero, cu excepția membru în picioare în rezoluția linie. (A se vedea Figura 2.)

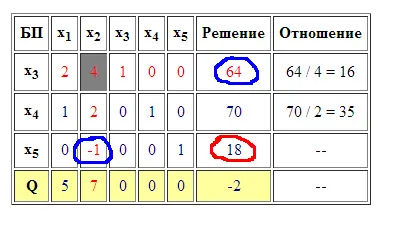
Celulele rămase din tabel (cu excepția „raportul“ coloana) sunt traduse în așa numita Regula dreptunghiului. sensul care este cel mai bine înțeleasă de exemplu. Să presupunem că trebuie să recalculeze elementul încercuite în contur roșu în figura 1. Mintal am tine-l pe verticală și pe orizontală până la intersecția, cu o rezoluție de autorizare a liniei și coloanei. Elementele care stau la intersecția circuitelor încercuite albastre (vezi Figura 1). Noua valoare a celulei „roșu“ va fi egală cu valoarea curentă a elementului minus produsul „albastru“ împărțit elementul permite ( „gri“) (vezi fig.1). Ie. 18 - (64 * -1) / 4 = 34. Aici semnul "*" este o operațiune de multiplicare.
Noi scrie noua valoare în poziție (a se vedea figura 2 contur roșu).

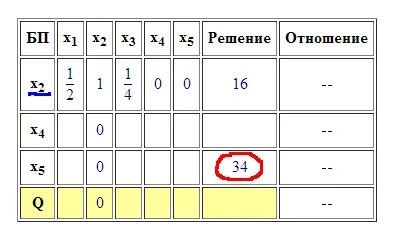
Folosind această regulă, vom umple toate elementele de masă goale (cu excepția coloanei „raportul“) a se vedea figura 3. Apoi, vom defini o nouă coloană care permite. Pentru a face acest lucru, să examineze șirul „Q“ și, deoarece sarcina noastră maximă, ne găsim în ea elementul pozitiv maxim. el determina care permite coloana. În cazul nostru este 3/2. Toate elementele indicate rezolvarea coloanei marcate cu roșu (vezi Fig.3). Dacă după următoarea iterație în șirul „Q“ nu va avea elemente pozitive - ceea ce înseamnă că se ajunge la soluția optimă, iterația terminată. Dacă scopul nostru a fost de a permite cel puțin coloana ar fi determinată de minimum de elemente negative, iar dacă după următoarea iterație din șirul „Q“ nu va apărea elemente negative, atunci se ajunge la soluția optimă.

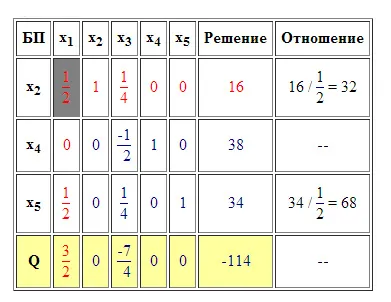
Acum completați coloana „atitudine“. Pentru aceasta, corespunzătoare (în picioare, în aceeași linie) „soluție“ element de coloană pentru a partaja în elementul corespunzător permițând coloanei (A se vedea figura 3). Notă. că operațiunea este efectuată numai pentru elementele pozitive care permit coloanei și linia „Q“ nu este implicat în această operațiune. În cazul în care, după o anumită iterație în coloana de eliberare nu va avea elemente pozitive, acest lucru este o sarcină imposibilă, având în vedere funcția obiectiv este nemarginit, iterație se oprește.

După umplerea coloanei „atitudine“, a defini o nouă rezoluție linie. Acesta este determinat de elementul minim al coloanei „atitudine“. În cazul nostru, această linie rezoluție 32. Toate elementele arătate în litere roșii (A se vedea Fig.3). În această iterație următoare se termină la următoarea iterație a x2 variabila este derivat din baza (acest lucru ne spune o nouă rezoluție a liniei), acesta va fi înlocuit cu un x1 variabilă (acest lucru ne spune noua coloană de autorizare) și toate calculele sunt repetate din nou.