Site personal - funcția y sin x, y cos x, y mf (x), y f (kx), y tg x, y ctg x

În continuare, vom forma un grafic. Se obține jumătate de undă, cel mai înalt punct al cărui (π / 2; 1). Acest grafic al funcției y = sin x în intervalul [0; π]. Adăugați la diagrame simetrice jumătate de undă (simetric în jurul originii, adică pe -π interval). Această jumătate de undă creasta - axa x cu coordonatele (-1, -1). Rezultatul este un val. Acest grafic al funcției y = sin x în intervalul [-π; π].

Puteți continua val prin construirea-l și pe intervalul [π; 3π], [π; 5π], [π; 7π] etc. In toate aceste segmente graficul functiei va arata la fel ca și pe intervalul [-π; π]. Se obține o linie ondulată continuă să aibă aceleași valuri.

Graficul unei funcții este o undă sinusoidală (este numit uneori cosinus).

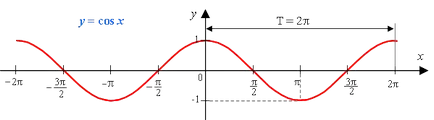
1) Domeniul funcției - setul de numere reale.

2) Domeniul de valori ale funcției - intervalul [-1; 1]

3) Aceasta este o funcție chiar.

4) Aceasta este o funcție continuă.

5) Coordonatele punctelor de intersecție ale graficului:
- cu abscisa: (π / 2 + πn; 0),
- cu axa ordonatei: (0; 1).

6) În intervalul [0; π] funcția scade, intervalul [tt; 2π] - crește.

7) La intervale [-π / 2 + 2πn; π / 2 + 2πn] Funcția ia valori pozitive.
La intervale [π / 2 + 2πn; 3π / 2 + 2πn] Funcția are o valoare negativă.

8) Lacunele cresc: [-π + 2πn; 2πn].
intervale descrescătoare: [2πn; π + 2πn];

9) punct minim: π + 2πn.
în funcție de punctul maxim: 2πn.

10) Această funcție este mărginită de mai sus și mai jos. Cea mai mică valoare funcției -1,
1, cea mai mare valoare.

11) Aceasta este o funcție periodică, cu o perioadă de 2π (T = 2π)

Ia functia y anterioara = cos x. După cum știți deja, graficul ei este o undă sinusoidală. Dacă vom multiplica funcția cosinus a unui anumit număr m, atunci unda se va extinde de la axa x (sau se contracta, în funcție de valoarea lui m).
Acest nou val și va graficul y = mf (x), unde m - numărul real arbitrar.

Astfel, functia y = mf (x) - este familiar pentru noi o funcție y = f (x), înmulțit cu m.

Efectuarea stretching sau de compresie, puteți construi mai întâi doar o jumătate de val undă sinusoidală, și apoi termina întregul program.

Dacă funcția y = mf (x) conduce la întindere a sinusoid axa x sau axa x la comprimare. funcția y = f (kx) conduce la o intindere de axa y sau axa y de compresie.

Și k - orice număr real.

Un program al acestei funcții, puteți construi mai întâi o jumătate de val undă sinusoidală, și apoi termina-l pe întregul program.

Graficul funcției y = tg x este tangensoida.

Este suficient să se construiască graficul în intervalul de la 0 la tt / 2, atunci acesta poate continua simetric în intervalul de la 0 la 3π / 2.

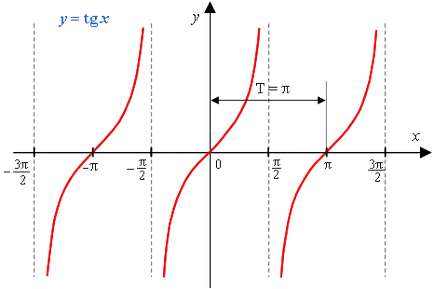
1) Domeniul funcției - mulțimea tuturor numerelor reale, cu excepția numerelor de forma
x = π / 2 + πk, unde k - este orice număr întreg.

Aceasta înseamnă că funcția grafic nu este punctul de care aparține unei linii drepte x = π / 2,
drepte sau x = 3π / 2, sau directă x = 5π / 2, sau directă x = -π / 2, etc.

2) valorile funcției Zona (-∞; + ∞)

3) Aceasta este o funcție impar.

4) Este o funcție continuă în intervalul (-π / 2; π / 2).

5) Aceasta este o funcție periodică, cu o perioadă π fundamentală (T = π)

6) Creșterile intervalul (-π / 2; π / 2).

7) Această funcție nu este limitată la partea de sus sau de jos. Ea nu are nici cel mai puțin, nici cele mai mari valori.

Graficul funcției y = ctg x este de asemenea tangensoida (uneori numit kotangensoidoy).

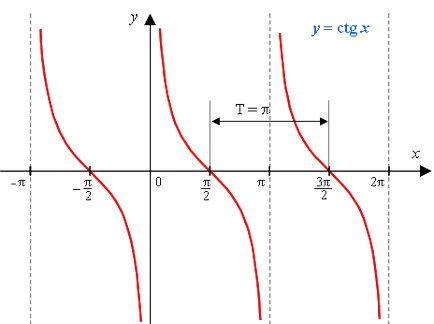
1) Domeniul funcției - mulțimea tuturor numerelor reale, cu excepția numerelor de forma
x = πk, unde k - orice număr întreg.

2) valorile funcției Zona (-∞; + ∞)

3) Aceasta este o funcție impar.

4) Aceasta este o funcție continuă.

5) Aceasta este o funcție periodică, cu o perioadă π fundamentală (T = π)

6) funcția scade în decalajul (πk; π + πk), unde k - este orice număr întreg.

7) Această funcție nu este limitată la partea de sus sau de jos. Ea nu are nici cel mai puțin, nici cele mai mari valori.