Sistemul spațial al forțelor

Momentul de forță în jurul axei este numită o valoare scalară egală cu momentul acestei forțe pe planul de proiecție perpendicular pe axa, luată în raport cu axa punctelor de intersecție cu avionul.

Pentru a găsi un moment de forță în jurul axei Z, trebuie (Figura 18.):

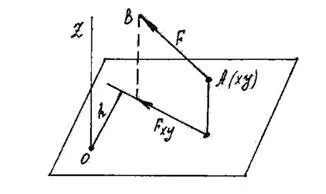
1) xy plane. perpendicular pe axa z;

2) să proiecteze o forță F pe planul, și pentru a calcula valoarea Fxy;

3) a redus din punctul O de intersecție al axei cu un plan perpendicular pe direcția Fxy h și lungimea acesteia;

4) calculează produsul Fxy · h;

5) determinarea punctului de marcaj.

Cazuri speciale la determinarea momentului:

1) dacă o forță paralelă cu axa, momentul său în jurul axei este egală cu zero, deoarece Fxy = 0;

2) Dacă linia forță de acțiune se intersectează axa, momentul său față de axa este, de asemenea, la zero, deoarece h = 0;

3) în cazul în care forța este perpendiculară pe axa, momentul său în jurul axei este produsul modulului forței la o distanță între forța și axa.

Condițiile de echilibru ale unui sistem spațial arbitrar al forțelor. Pentru a echilibra un sistem spațial arbitrar al forțelor este necesar și suficient ca suma proiecțiilor tuturor forțelor pe fiecare dintre cele trei axe și suma momentelor lor în ceea ce privește aceste axe sunt egale cu zero.

Rezolvarea problemelor. În primul rând, trebuie să luăm provocarea:

1) stabilește echilibrul organismului trebuie luate în considerare în această problemă;

2) să identifice corpul și tratarea acestuia ca liber, atașați la ea toate forțele care acționează asupra corpului și reacția conexiuni a scăzut;

3) crearea condițiilor de echilibru, folosind forma acestor condiții, ceea ce conduce la o soluție mai simplă.

Pentru mai multe ecuații simple, astfel:

1) făcând proiecții ale ecuației, pentru a efectua o coordonată axă perpendiculară pe o anumită forță necunoscută;

2) care alcătuiesc ecuația de momente, momente pentru a lua în centrul atenției la punctul în care se intersectează mai multe forțe necunoscute.

Solutia multor probleme staticii reduse la determinarea reacțiilor de sprijin, prin care fixa grinzi, rame, grinzi de pod, etc.

Tehnica întâlnite cel mai frecvent următoarele trei tipuri de fixare de sprijin.

1. balamale mobile suport (fig. 19).

Acest suport oferă doar o singură reacție de referință - RA. care este direcționat de-a lungul comune normală la suprafețele portante.

2. suport fix articulat (Fig. 20). Reaction NA un astfel de suport este direcționat într-un plan arbitrar. Pentru comoditatea de rezolvare a problemelor este răspândit în două componente - RA și HA: